Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 10. 2010 22:55 — Editoval Frantik88 (20. 10. 2010 22:57)
Matematická indukce
Dokazte, ze  pro
pro  .
.
Udělal jsem základní krok, tedy:
Když  , pak tedy
, pak tedy  , to jest
, to jest 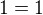 , tudíž základní krok platí!
, tudíž základní krok platí!
Indukční krok:


A teď už nevím kam dál :-(.
Nevím, zda-li jsem postupoval správně, či jsem někde udělal chybu.
********
********
* O = O *
_
Offline
#5 20. 10. 2010 23:42
Offline
#9 20. 10. 2010 23:52
Re: Matematická indukce
↑ Frantik88:
Mozno pomoze, ked si trochu sprehladnime ten dokaz. Indukcny predpoklad je, ze  . Teraz chceme dokazat, ze
. Teraz chceme dokazat, ze  , pricom mozme vyuzit, ze plati indukcny predpoklad.
, pricom mozme vyuzit, ze plati indukcny predpoklad.
Takze samotny dokaz:  .
.
Tu prvu nerovnost dostavame tak, ze len vynasobime obe strany nerovnosti v indukcnom predpoklade (kladnym) vyrazom (n+1), ta druha nerovnost plati, pretoze  .
.
Offline
#12 21. 10. 2010 00:30
Re: Matematická indukce
↑ Frantik88:
Tak na to koukám a zdá se že 0^0 může být i 1, záleží na kontextu a definici. Beru zpět.
Offline


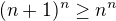 ?
?

 nedefinujeme, zřejmě mysleli čísla
nedefinujeme, zřejmě mysleli čísla  .
.