Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2008 17:02 — Editoval NetFenix (02. 04. 2008 17:47)
Komplexní čísla
Zdravím,
chtěl bych se zeptat, jak se dá počítat s komplexními čísly.
A to když potřebuju:
1) spočítat například cosh, sinh a argument je komplexní číslo;
2) když mám nějaké reálné číslo a mocnitel je komplexní číslo
3) a odmocnina z komplexního čísla
Nevím jestli jsem to jasně popsal, takže potřeboval bych se naučit, jak pomocí tužky, papíru a jednoduché kalkulačky dojít k výsledkům z těchto operací, např.:
sqrt(1+i)
2^(1+i)
sinh(1+i)
cosh(1+i)
Koupil jsem si schválně kalkulačku, která umí komplexní čísla, ale pouze základní operace s nimi. Nyní toto počítám v Matlabu, ale nemyslím, že mi dovolí tento program používat při písemce:-)
Děkuji moc za rady
Offline
#2 02. 04. 2008 22:58
Re: Komplexní čísla
1) Využiju součtové vzorce pro hyperbolické funkce:
http://cs.wikipedia.org/wiki/Hyperbolick%C3%A1_funkce
Potom
Prosím překontrolujte to po mě někdo…
2) složitější, výsledek není jednoznačný, ale lze využít Eulerových vzorců, takže "zhruba platí"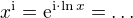
Offline
#3 03. 04. 2008 14:33
Re: Komplexní čísla
Díky za pomoc, strašně mi to pomohlo z toho co jste mi poradil, jsem snad i nějak došel k tomu jak spočítat odmocninu, ale raději to tu ještě napíšu, jestli tento postup může být správný.
Konkrétní příklad: 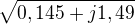
Absolutní hodnota: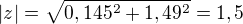
Úhel: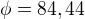
Z toho dále dostanu: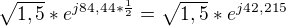
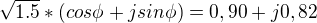
Jde mi hlavně o to jestli je to správný postup. Kdyby na to někdo hodil oko a odouhlasil mi, že by to takto mohlo být, byl bych určitě rád.
Offline
#4 03. 04. 2008 19:27
Re: Komplexní čísla
Jo, postup je více méně správně. Ale pozor, jestliže jste si zvolil  jako úhel toho původního čísla, pak musí být v argumentu těch goniometrických funkcí
jako úhel toho původního čísla, pak musí být v argumentu těch goniometrických funkcí 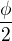 .
.
Jenže pozor: Všimněte si, že když k  přičtete 180°, hodnota původního čísla se nezmění, ale po vydělení tohoto úhlu dvěma dostanete jiné číslo. I toto je platný výsledek odmocňování. Jde o to, že n-tá odmocnina má v komplexních číslech n různých hodnot, které tvoří na Gaussově rovině vrcholy rovnostranného n-úhelníka se středem v nule, pro druhou odmocninu jsou to pak 2 opačná čísla.
přičtete 180°, hodnota původního čísla se nezmění, ale po vydělení tohoto úhlu dvěma dostanete jiné číslo. I toto je platný výsledek odmocňování. Jde o to, že n-tá odmocnina má v komplexních číslech n různých hodnot, které tvoří na Gaussově rovině vrcholy rovnostranného n-úhelníka se středem v nule, pro druhou odmocninu jsou to pak 2 opačná čísla.
Offline
 , aby to vyšlo. Nicméně normálně se to dělá až v těch argumentech, jak jste uvedl.
, aby to vyšlo. Nicméně normálně se to dělá až v těch argumentech, jak jste uvedl.