Matematické Fórum

↑↑ ttopi:
Pokud jedou za sebou nemají stejný čas ale dráhu. (asi jen překlep)

Takže jsem si s dovolením přivlastnil myšlenku od ttopi a trochu ji opravil. (ttopi promiň)

U těchto typů úloh je důležité, co mají auta společného.

a) Pokud jedou za sebou, mají společnou dráhu, protože jedou stejným směrem a někde se setkají, čili ujedou oba stejně.

b) Pokud jedou proti sobě, mají společný čas, protože se za nějaký čas potkají a je jedno jakou jede kdo rychlostí.

↑↑ Syslinho15:
Pokusím se ti to vysvětlit trochu obšírněji:
Označme:
s -     vzdálenost Praha - Bratislava (360 km)
s_1 - vzdálenost Praha - místo setkání (máme určit)
v -     celková rychlost aut
v_1 - rychlost auta jedoucího z Prahy (80 km/h)
v_2 - rychlost auta jedoucího z Bratislavy (70 km/h)
t -     celkový čas setkání (máme určit)
Můžeme tedy sestavit rovnice:

1)
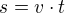
2)
3) 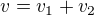  celková rychlost aut je součtem jednotlivých rychlostí, protože auta jedou proti sobě

Z rovnice 1) vyjádříme čas t
4)
Do rovnice 4) dosadíme rovnici 3)
5) - celkový čas, za který se auta srazí
Do rovnice 2) dosadíme čas t z rovnice 5) a vypočteme vzdálenost aut od Prahy
6)

Teď už stačí dosadit do rovnic 5) resp. 6) známé hodnoty a vypočítat to na co se nás ptají.



Auta se setkají za 2 hodiny 24 minut od výjezdu ve vzdálenosti 192 km od Prahy.

Tak, jdeme na to.

Víě, že cesta z bodu A do bodu B (dále budu značit 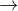) trvá 2h a 54minut, čili 2,9h.

Vzoreček pro čas je .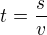
Víš, že cesta má 3 úseky, přičemž každý se jde jinou rychlostí a každý má svou délku - ty označím jako , přičemž vím, že .

Takže dostávám první rovnici:


Cesta zpět trvala 3h a 6 minut, což je 3,1 hodin.
Víme ale, že zpět se jde nejprve po úseku s_3 ale rychlostí v_1 což je rychlost do kopce, úsek s_2 je stejný pro obě trasy, protože je rovný. Úsek s_1 se jde při zpáteční cestě z kopečka, takže rychlostí v_3.

Opět sestavím rovnici:


V obou rovnicích mám sice 3 neznáme, ale lehce to vyřešíme. Jelikož , tak z toho vyjádřím, že a dosadím.

Celkem mám soustavu 2 rovnic o 2 neznámých, která vypadá takto:

Vynásobím obě rovnice 60 a dále upravuju. Posčítám co se dá a nakonec vyleze postupně 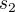, pak a nakonec .


Mě tedy vyšlo, že první úsek je dlouhý 3km, druhý 4km a třetí 4,5km - vyšla i zkouška.

↑ martas277:

Super, co mi dáš za známku? :-)

smícháním polotučného a plnotučného mléka v poměru 1:2 získáme mléko, které obsahuje 30g tuku v každém litru, kdežto smícháním v poměru 2:1 získáme mléko s 25g tuku v 1 litru.kolik g tuku obsahuje 1 l plnotučného mléka? já jsem to řešil takhle:

1y/2x=30
2y/x=25             kde je chba?

je, ale proč jste to dělil třemi?

Asi jsem nezvolil dobrý přístup. Tak jinak.

Při poměru 1:2 je jasné, že nejmenší počet litrů mléka po smíchání je 3(1+2). Nebo to může být 6(2+4) nebo 9(3+6) - vždy ale musí být poměr 1:2.

Proto beru ten nejjednodušší případ, že mám na konci 3 litry - 1 polotučného a 2 litry plnotučného.

Pak vím, že neboli 1 litr s X obsahem, k tomu 2litry s Y obsahem a celkem mám 3 lytry s 30g obsahem.

Už je to lepší?

potřepuji pomoct s tímto příkladem: Po okruhu dlouhém 2500m jezdí dva motocykly. potkávají se každou minutu , jezdí-li proti sobě, a míjejí se každých 5 min, jezdí-li týmž směrem. Určete jejich rychlosti za předpokladu, že jsou stálé a nezávislé na směru jízdy.

diky je to dobře

Sakra, byl jsem doučovat a celou cestu se těším, jak napíšu svůj výpočet, ale už to nemá cenu, je prakticky stejný, jako ten Chrpův :-)

Ale přecijen něco. Tu rovnici musí žák základní školy cítit jako vyplivnutou. Je potřeba to více vysvětlit.

Čili takto bych na to šel já:

Vím, že ten pomalejší ujede rychlostí 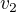za 300 sekund úsek
Ten rychlejší, aby se mohli potkat, ho musí vždy předjet o kolo. Takže ujede celé kolo, což je 2500m a + to, co ujede ten pomalejší a to rychlostí .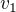
Jelikož se časy rovnají, napíšu to do rovnice.


Z toho už vyleze, že


Tímto se omlouvám Chrpovi, pokud se bude cítit ukřivděný, ale jsem si opravdu jist, že by málokdo pochopil, poroč je například u té druhé rovnice v závorce 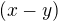. Nakonec to vyleze stejně, ale opravdu na základní škole je třeba si uvědomit, že takové rovnice a počty vidí poprvé v životě a těžko hned pochopí, že to takhle bude vypadat.

EDIT: Jinak k tomu doučování. Konečně poznávám, zač je toho loket. Učím kluka šikovného a chápavého, ale přesto jsem se zapotil, než jsem mu pořádně vysvětlil, že když nanášim zprava 60°, tak pak nemůže jako úhel označit ten vedlejší, čili těch 120°. My vidíme na první pohled, která bije, ale ti žáci to opravdu vidí poprvé a je to pro ně nová vesnice, kde je musíte krůček po krůčku provést a nic nevynechat.

Dalším menším problémem bylo grafické sčítání a odečítání úhlu. Než si uvědomil, kam se musí nanášet úhly při sčítání, respektive odečítání, dalo to zabrat. Pak stačilo otočit počátek nanášení úhlů a už z toho byla chyba.

:-)

↑ ttopi:

Zdravím :-)

Ivana přála k tvému dosažení Q v tématech účitelů (to bych si netroufla, ale zde u doučovatelů ráda bych se připojila k oslavným projevům a přeji, at dokážeš vše, nač si vzpomeneš :-)

Občas právě od tebe dostávam napoměnutí, ať nejsem drzá, tak reaguji závěrečnou větou hrdiny filmu, který posílám, jako malý dárek: "Ребята, давайте жить дружно!" - musíš ale dodívat až do konce :-)

Kolegu Chrpu zdravím také :-)

potřeboval bych vysvětlit tento příklad:  Z opačných konců trasy dlouhé 50km vyšli ve stejný okamžik dva dálkoví chodci a pohybovali se stálými rychlostmi. Setkali se po 5h chůze. Pak pokračovali v původních směrech pochodu tak, že první chodec snížil svou rychlost o 1km/h, druhý chodec naopak svou rychlost o 1km/h zvýšil. První chodec dorazil do cíle o 2h dříve než druhý chodec. Určete rychlosti obou chodců do okamžiku setkání.

↑ martas277:

Zdravím :-)

zkus se podívat na příspěvek 57, 58. http://forum.matweb.cz/viewtopic.php?id=3424&p=3  OK?