Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 04. 2008 19:42
Zvlastni rovnice
ahoj, nedavno sme ve skole pocitali nejakou kombinatoriku, a udelal chybu v jednom prikladu a dostal sem se k nasledujici rovnici:
na presnym zadani uplne nezalezi, ale de mi o to jestli existuje nejakej stredoskolskej zpusob jak tutu nebo podobnou rovnici resit. nic me nenapadlo, protoze to je vlastne polynom x-tyho stupne, a cely je to nejaky divny. je tu nekdo kdo by mi osvetlil reseni?
Offline
#3 07. 04. 2008 20:23
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Zvlastni rovnice
mhm, jak by se ty logaritmy pokrátily?
Offline
#4 07. 04. 2008 20:37
Re: Zvlastni rovnice
↑ robert.marik:
myslel jsem to takto : 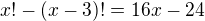

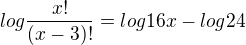
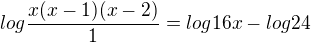
ale jak jsem psal, je to jen úvaha, zřejmě to není dobrá úprava kdyžtak mě oprav, budu rád
Offline
#6 07. 04. 2008 21:23
Re: Zvlastni rovnice
Pratele stredoskolaci, ta rovnice neni nijak tezka, zapomente na logarimty a podobe skopiciny a zapojte mozkovny. Kdo to vyresi do pulnoci ma u mne plus.
A vysokoskolaci (at uz studenti nebo ucitele) to sem hned nevykecjte at si ostatni muzou zapremyslet.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#7 07. 04. 2008 21:36 — Editoval Ginco (07. 04. 2008 21:36)
#9 07. 04. 2008 21:52
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Zvlastni rovnice
↑ Lishaak:
Nevím, jsem středoškolák a po odpadnutí veškeré mozkovny jsem to vzal postupně. Dosazováním :) Jelikož je Df {3, 4, 5, ... }, vzal jsem čísla 3-6 a žádné nevyhovovalo a levá strana rovnice se začala příliš zvyšovat oproti té pravé. Pokud jsem nikde neudělal chybu, tak to nemá řešení. Matematicky to však nedokážu. Jen aby tu nebyl přílišný hon za odpovědí.
Offline
#11 07. 04. 2008 22:14
Re: Zvlastni rovnice
↑ Lishaak: Takhle mi vzit vitr z plachet.. :-)
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#12 07. 04. 2008 22:30
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Zvlastni rovnice
↑ Lishaak:
Tak to mohu polozit rovnou nerovnici x(x-1)(x-2) > 16x - 24 (pri predpokladu, ze (x-3)! je kladné a Df je 3, 4, ...), nebo neco v tom zpusobu
Offline
#13 07. 04. 2008 22:31 — Editoval Alesak (07. 04. 2008 22:35)
Re: Zvlastni rovnice
↑ Lishaak:
hmm, podle me by stacilo z toho udelat x! > 16x, protoze (x-3)! je vetsi nez 0 a u 16x - 24 muzeme tu 24 vypustit protoze nam to ten graf stejne akorat posune dolu. takze mame (x-1)! > 16 coz uz se da z hlavy zpocitat. z cehoz plyne ze se obe strany rovnice uz nikdy neprotnou.
takle numericky resit je obvzlast faktorialy docela lehky, kdyz x nalezi N a jeste nejspis nebude o moc vetsi nez treba 10. me spis ale zajimalo jestli by s tim nesel udelat nejakej trik aby z toho vylezla nejaka normalni rovnice a aby nam treba vyslo x = -3 nebo 1/2=7 nebo tak neco.
taky sem koukal na wikipedii, a i kdyz nam to moc nepomuze tak myslim ze to je docela zajimavy. to ze se da faktorial aspon priblizne vyjadrit nejakym funkcnim vztahem. btw to pi se taky vetre vsude, dokonce i k faktorialum.
Offline
#14 07. 04. 2008 22:35 — Editoval Ginco (07. 04. 2008 22:53)
Re: Zvlastni rovnice
pravá strana rovnice je vlastně aritmetická posloupnost : 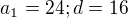
Pokud vezmu 6! + (6-3)! > a_1 + 3d
vezmu fci y = x! + (x-3)!
Vím, že D(f) = {3;4;5;...}
vím, že tato fce bude jen v 1. kvadrantu a také vím, že to bude část paraboly
vezmu fci y' =16x - 24
Tato fce bude také v 1. kvadrantu a víme, že grafem je přímka
V tomto případě graf fce y(paraboly) je rychleji rostoucí než graf fce y' ( přímky), Pro x= 5 je y mnohem více rostoucí než y', tudíž pro žádné x>5 neexistuje řešení.
Ty 2 fce se protnou,ale jak již bylo zmíněno to nenáleží do oboru přirozených čísel
Je to asi blbost, ale nic víc mě nenapadlo
Offline
#15 08. 04. 2008 08:27
Re: Zvlastni rovnice
Nejblize k velmi hezkemu reseni je podle me sam ↑ Alesak:. Je to receno trosku mlhave, takze sem napisu, jak bych to zapsal ja:
Pro 'x' z moziny {5, 3, 7, 8, ...} jiste plati nerovnost
(x-1)! > 16
Tedy take plati
x! > 16x
Protoze (x-3)! + 25 je urcite kladne cele cislo, potom taky plati
x! + (x-3)! + 25 > x! > 16x
a tedy
x! + (x-3)! > 16x - 25.
Cili je jasne, ze zadne 'x' vetsi nez 4 nemuze byt resenim rovnice. Staci jiz tedy vyzkouset cisla 3,4, pro ktera rovnice take neplati.
Toto je podle me velmi nazorne a jednoduche zduvodneni toho, ze rovnice nema zadne reseni v oboru prirozenych cisel. Gratulace Alesakovi.
Tady bych rad zduraznil, pro ty, kteri se chteji matematikou vie zabyvat, ze vetsina problemu z "praxe", tedy takovych, ktere nebyly vymysleny jako cvicne priklady do nejake ucebnice nebo pisemky, ale vyvstaly z potreby resit nejaky skutecny problem, maji prave tento charakter. Je u nich vzdy treba zmobilizovat vlastni duvtip a vymyslet originalni reseni, nebot obecny vzorec mnohdy ani neexistuje.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#17 08. 04. 2008 16:32
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Zvlastni rovnice
↑ Lishaak:
To je ale same kdyby, jakoby, jista cast Df, nejspis a tak. Sice to jsou vsechno pravdy, ale cekal jsem spise nejaky opravdu matematicky dukaz. Ne ze by to bylo nespravne, ale jen se mi to nezda. Pripomina mi to moje alternativni postupy, ktere se zatim nelibily zadnemu z profesoru :)
Offline
#18 08. 04. 2008 16:53
#19 08. 04. 2008 19:30
Re: Zvlastni rovnice
↑ halogan:
Mejak se mi nedari porozumet tomu, cos chtel tim prispevkem presne rict
halogan napsal(a):
To je ale same kdyby, jakoby, jista cast Df, nejspis a tak.
Teto vete opravdu nerozumim, at se snazim sebevic.
halogan napsal(a):
Sice to jsou vsechno pravdy, ale cekal jsem spise nejaky opravdu matematicky dukaz.
Zkus vic specifikovat, co si predstavujes pod pojmem matematicky dukaz. Me tenhle prijde celkme pekny, a jak sam rikas, vsechno jsou to pravdy.
halogan napsal(a):
Pripomina mi to moje alternativni postupy, ktere se zatim nelibily zadnemu z profesoru :)
Tak byly asi spatne ;-). Pokud mas primo konkretni priklad takoveho postupu, rozhodne ho sem napis a urcite o nem podiskutujeme.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#20 08. 04. 2008 19:49
Re: Zvlastni rovnice
↑ Lishaak:
rek bych ze by je zajimalo jestli by to slo nejak upravit na tvar x = neco. me by to teda taky zajimalo, i kdyz nevidim zpusob jak to udelat
Offline
#21 08. 04. 2008 20:01
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Zvlastni rovnice
↑ Alesak:
Asi tak :)
↑ Lishaak:
Holt mam problemy s vyjadrovanim :) Ja jsem sam zastance logicky vyvodeni jako reseni, ale ucitele po nas pozaduji vice vedecke (matematicke) reseni, takze by se jim podle me nelibilo reseni tve. Ale co ja vim. A co ja vim, zda je vubec jine reseni.
K mym postupum - samozrejme myslim jen kdyz jsou spravne :)
Offline
#22 08. 04. 2008 20:23
Re: Zvlastni rovnice
Pardon, nečetl jsem tu diskusi předtím, ale moje řešení - vidím, že levá strana roste "v konečném důsledku" mnohem rychleji než pravá, určitě tedy existuje nějaká mez, za kterou už nemá cenu hledat řešení. Tudíž je nalezení řešení triviální záležitostí, kterou za nás udělají stroje.
(Takhle já řeším většinu věcí…)
Offline
#23 09. 04. 2008 10:11
Re: Zvlastni rovnice
↑ Olin:
Nemuzu se ubranit tomu, abych na tohle reagoval. Ja se obecne nebranim tomu, aby mechanicky narocne priklady resily stroje. Bylo by hrichem nevyuzit moderni techniky, kdyz uz ji tady mame. Tem, kteri by radi prenesli na stroje veskere ulohy, ktere vyzaduji byt jen minimum premysleni vsak doporucuji zamyslet se nad temito fakty:
1. Nekdo ty stroje musi stavet/programovat, tudiz stale budou potreba lide, kteri tomu musi opravdu do hloubky rozumet.
2. Resit tuhle rovnici strojove (tedy psat program, ktery otestuje rozumna reseni) je alespon tak pracne, jako tu rovnici vyresit uvahou. Cili vseho s mirou, netreba brat hned kanon na vrabce.
3. Budeme-li se mene spolehat na stroje, mame vetsi sanci, ze objevime novy postup, pomoci ktereho budeme schopni resit celou novou tridu problemu, na jejichz reseni bychom jinak museli psat programy pro kazdou takovou ulohu zvlast.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
