Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 04. 2008 21:18
parádní úloha
Našel jsem v knížce o A. Einsteinovi zajímavou úlohu z dob renesance
Kateřině je 24 let.
Je dvakrát tak stará, jako byla Anička v době, kdy Kateřině bylo tolik let, kolik je Aničce teď.
Kolik let je Aničce ?
chtěl bych aby ste hned neposílali řešení, řekněme tak okolo půl jedenácté, a? mají všichni čas si zapřemýšlet.
Chtěl jsem Haloganovi vynahradit tu včerejší úlohu
Offline
#2 08. 04. 2008 21:42 — Editoval halogan (08. 04. 2008 21:53)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: parádní úloha
To je tak genialne jednoduche zadani, az se v nem neuveritelne ztracim :)
Edit: reseni jsem vzal velice vedecky, protoze jsem nerozumel zadani. Tak jsem zvedav na reseni ostatnich :)
Offline
#4 08. 04. 2008 22:31
Re: parádní úloha
↑ Ginco:sestavím rovnici : 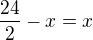
... x=6 . Před 6ti lety bylo Kateřině 18 let a byla dvakrát tak stará jako byla Anička .Tehdy bylo Aničce 9 let . Nyní je Kateřině 24 let a Aničce je tudíž (9+6) ... 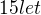 .
.
Jsou moje úvahy správné ?
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#8 08. 04. 2008 22:57
Re: parádní úloha
↑ Ginco:Tak to zkusím ještě jednou : 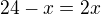
pak x =8 ... Před 8lety bylo Kateřině 16 let , Aničce 8 let . Což je dvojnásobek věku Aničky v té době. Nyní je Kateřině 24 a Aničce též o 8 let více tudíž 16 let .
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#13 08. 04. 2008 23:13
Re: parádní úloha
↑ halogan:
Taky jsem si to zadání vyložil tímto způsobem.
Hold, to už je slovíčkaření, ale pravdou je, že čas v zadání je použit přítomný.
Offline
#16 08. 04. 2008 23:16
Re: parádní úloha
↑ Ginco: Tak tohle vypadá důvěryhodně , máš řešení i v knížce ? Já jsem k těm 18 ti přišla také ale jenom dedukcí . Vypočetla jsem si z jednoduché rovnice x a vyšlo mi 6 a pak jsem jen kombinovala . Ale tahle rovnice je opravdu parádní . :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#25 09. 04. 2008 18:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: parádní úloha
↑ Ginco:
Pokud se nemylim, tak v Babylonu byla zakladem systemu poctu 60 a tak se orientovali na deliteli 60. Coz v nasem zadani mame na prave strane rovnice. Pak uz by to nemel byt problem :-)
Offline



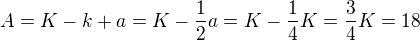
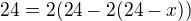
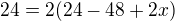
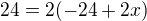
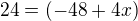
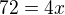
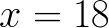


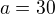
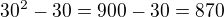 .. 870=14*60+30 .. Strana je dlouhá 30 .
.. 870=14*60+30 .. Strana je dlouhá 30 .