Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 12. 2010 12:56
konstrukcia trojuholnika
Ahojte, mam tu jednu konstrukcnu ulohu s ktorou neviem ako zacat:
Zostrojte trojuholnik ABC ktory ma tieto vlastnosti : |BC| : |AC| = 2:3 ; vc=4cm ; uhol gama = 60 st.
zacal som tak ze som si oznacil strany BC=2x ; AC=3x. A dalej som sa nedostal, skusal som cez kosinusovu vetu riesit ale neviem ako dalej, poradte mi.
Offline
- (téma jako vyřešené označil(a) faktorial)
#2 14. 12. 2010 13:32
Re: konstrukcia trojuholnika
Využiješ podobnosť trojuholníkov..Všetky trojuholníky, ktorých pomer strán |BC|:|AC| je 2:3 a uhol gamma je 60 stupňov, sú podobné. Narysuješ jeden takýto trojuholník a teraz predĺžíš jeho strany a výšku, aby mala 6 cm a narysuješ trojuholník ABC.
1^6 - 2^6 + 3^6 = 666
Offline
#4 14. 12. 2010 15:54 — Editoval BakyX (14. 12. 2010 16:34)
Re: konstrukcia trojuholnika
Ak by niekoho zaujímal výpočet.
Poznáme: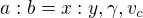
Najprv použijeme vzorce pre výpočet obsahu trojuholníka:
Vytvoríme rovnosť z ktorej vyjadríme "c"
Keďže 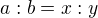 môžme tvrdiť, že
môžme tvrdiť, že 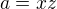 a
a 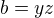 . Dosadíme toto všetko do kosínovej vety. Snažíme sa vyjadriť "z".
. Dosadíme toto všetko do kosínovej vety. Snažíme sa vyjadriť "z". 
Potom ale:
Na základe údajov z tvojho zadania:
1^6 - 2^6 + 3^6 = 666
Offline
