Matematické Fórum

osamela · 27. 12. 2010 20:32

Nalezněte souřadnice vrcholů trojúhelníku ABC, znáte-li středy K[ 1 ,6], L[-4, 2], M[3 , -2] , jeho stran BC, AC, AB. Toto je zadání příkladu znám vzoreček pro výpočet souřadnic středu S= A+B/2 , ale nevím jak dál jestli přes nějakou soustavu rovnic ... nemohu na to přijít . Děkuji za radu.

teolog · 27. 12. 2010 21:30

↑ osamela:
Podobný příklad se řešil zde.

Chrpa · 27. 12. 2010 22:14 — Editoval Chrpa (28. 12. 2010 13:03)

↑ osamela:
Řešil bych to takto:
1) Strana AB je rovnoběžná s přímkou KL a prochází bodem M
2) Strana AC je rovnoběžná s přímkou KM a prochází bodem L
3) Strana BC je rovnoběžná s přímkou LM a prochází bodem K
4) Bod A je průsečík přímek AB a AC
5) Bod B je průsečík přímek AB a BC
6) Bod C je průsečík přímek AC a BC
Pokud jsem dobře počítal tak:

Autor skryl část textu. Zobrazit/skrýt!

jelena · 28. 12. 2010 09:23

Zdravím vás, proč jste neřešili soustavu rovnic:

(b+c)/2=1
(a+c)/2=-4
(a+b)/2=3

a, b, c jsem označila x-souřadnice bodu A, B, C? podobně pro y-souřadnice. Děkuji.

Cheop · 28. 12. 2010 09:52 — Editoval Cheop (28. 12. 2010 10:02)

↑ jelena:
Zdravím,
protože nás to nenapadlo.
Proč to dělat jednoduše když to jde složitě?
Rovnicemi to vychází překvapivě stejně jako mým postupem
přes průsečíky stran

jelena · 28. 12. 2010 10:19

↑ Cheop: proč překvapivě? :-) Kolegyňka ↑ osamela: soustavu navrhovala hned na úvod.

Děkuji. Tak u nás sněží :-)

Cheop · 28. 12. 2010 11:07

↑ jelena:
To já píšu jen tak, že překvapivě
Jinak to přeci musí vyjít stejně.

osamela · 28. 12. 2010 15:43

↑ Cheop: ano myslela jsem na ní, jen jsem si nebyla jistá..vyzkoušela jsem a sedí to moc děkuji za spolupráci

jelena · 10. 01. 2013 19:43

Zdravím v tématu, byla jsem požádána o vysvětlení asi tohoto:

Zdravím vás, proč jste neřešili soustavu rovnic:

(b+c)/2=1
(a+c)/2=-4
(a+b)/2=3

a, b, c jsem označila x-souřadnice bodu A, B, C? podobně pro y-souřadnice. Děkuji.

Pokud znám souřadnici středu úsečky, potom mohu předpokládat, že střed byl vypočten ze souřadnic krajních bodů úsečky dle vzorce pro střed úsečky, tedy 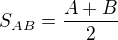$S_{AB}=\frac{A+B}{2}$ , presne 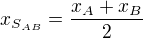$x_{S_{AB}}=\frac{x_A+x_B}{2}$ obdobně y-souřadnice. Z toho mám navržený systém rovnic.

jelena · 10. 01. 2013 20:44

M[3 , -2] je střed AB, tedy 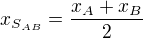$x_{S_{AB}}=\frac{x_A+x_B}{2}$ dosazuji: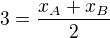 $3=\frac{x_A+x_B}{2}$

L[-4, 2] je střed AC, dosazuji 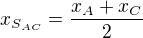$x_{S_{AC}}=\frac{x_A+x_C}{2}$ dosazuji: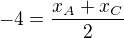 $-4=\frac{x_A+x_C}{2}$

Poslední rovnic již zvládneš. Dosazuj, prosím. A piš, prosím, do tématu - to je větší jistota, že se to všimne, než PM.

Studovina

Nejspíše jsem špatně vysvětlil, kde mám problém. Toto ještě chápu, ovšem zde už končím. Nejspíše jsem naprosto špatně pochopil, jak mám postupovat.

například u středu úsečky AB 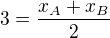$3=\frac{x_{A}+x_{B}}{2}$ nevím jak pokračovat, napadlo mě, že bych mohl vypočítat 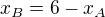$x_{B}=6-x_{A}$ ovšem když toto poté dosadím do rovnice, tak se mi 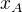$x_{A}$ mezi sebou odečtou a vznikne nula...

jelena · 10. 01. 2013 21:04

↑ Studovina:

sestav, prosím, celou soustavu. Tato úprava 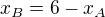$x_{B}=6-x_{A}$ je dobra pro 1. rovnici, dosazovat však budeš do jiné, ne do první rovnice. Jinak může použit jak metodu sčítací, tak dosazovací.

Já už bych ale, prosím, dělala něco jiného. Ať se podaří.

Studovina · 10. 01. 2013 21:19

↑ jelena:
Moc děkuji za radu. Konečně mi mozkové závity roztály a mě docvakla tvoje rada. Už to začíná jít jako po másle :-)

Matematické Fórum

#1 27. 12. 2010 20:32

vektory

#2 27. 12. 2010 21:30

Re: vektory

#3 27. 12. 2010 22:14 — Editoval Chrpa (28. 12. 2010 13:03)

Re: vektory

#4 28. 12. 2010 09:23

Re: vektory

#5 28. 12. 2010 09:52 — Editoval Cheop (28. 12. 2010 10:02)

Re: vektory

#6 28. 12. 2010 10:19

Re: vektory

#7 28. 12. 2010 11:07

Re: vektory

#8 28. 12. 2010 15:43

Re: vektory

#9 10. 01. 2013 19:43

Re: vektory

#10 10. 01. 2013 20:44

Re: vektory

#11 10. 01. 2013 20:56 — Editoval Studovina (10. 01. 2013 20:57)

Re: vektory

#12 10. 01. 2013 21:04

Re: vektory

#13 10. 01. 2013 21:19

Re: vektory

Zápatí