Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 01. 2011 11:08
Logaritmická rovnice 4.
Všichni se v něčem předstihujeme, proto se od sebe učíme, je to lidské, nic lidského mi není cizí ... ;)
Offline
- (téma jako vyřešené označil(a) calis)
#3 07. 01. 2011 11:19 — Editoval hradecek (07. 01. 2011 11:24)
Re: Logaritmická rovnice 4.
↑ calis:
Použiješ pravidlo 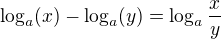 a
a 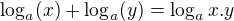
Dostaneš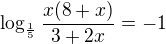
Ďalej vieš, že platí: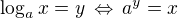
Takže: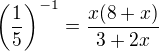
Dostaneš kvadratickú rovnicu t.j. dva korene. Z podmienky zistíš, ktoré z koreňov rovnici vyhovujú.
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#4 07. 01. 2011 11:24
Re: Logaritmická rovnice 4.
↑ hradecek: ok zkusím a pošlu výsledek ;)
Všichni se v něčem předstihujeme, proto se od sebe učíme, je to lidské, nic lidského mi není cizí ... ;)
Offline

