Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita integrálního součtu (TOTO TÉMA JE VYŘEŠENÉ)
#2 24. 04. 2008 12:15
Re: Limita integrálního součtu
↑ Pavel.R:
Ahojky, přiznám se, že mi přijde zvláštění ten součet řady, ale fakt nevím. Zkoušela jsem to pomocí částečných součtů - sečíst první a poslední, vynásobit n a to celé vydělit 2 a z toho limitu, vyšlo mi 128. :-)
Offline
#3 24. 04. 2008 22:19 — Editoval robert.marik (24. 04. 2008 22:24)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Limita integrálního součtu
↑ nika.v:
koušela jsem to pomocí částečných součtů - sečíst první a poslední, vynásobit n a to celé vydělit 2 a z toho limitu, vyšlo mi 128.
no nevím..... jak se vlastně sčítá řada 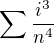 ? určitě ne stejně jako aritmetická řada.
? určitě ne stejně jako aritmetická řada.
Offline
#4 24. 04. 2008 22:33
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Limita integrálního součtu
nakonec jsem to nacpal do Maximy
sum(k^3, k, 1, n), simpsum; -> ((4*n-1)^4+2*(4*n-1)^3+(4*n-1)^2)/4
po vydeleni n^4 a limitnim prechodu n->nekonecno vychazi 64
hodnota toho integralu pres primitivni funkci je taky 64
chce to jenom umet odvodit ten vzorec na soucet te rady. Byl na to nejaky umely trik, ted ale nemam cas ho hledat ....
Offline
#5 25. 04. 2008 01:04
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Limita integrálního součtu
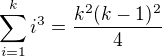 (existuji spousty zpusobu, jak toto dokazat, napr. kdyz uz vzorec tahto "uhodneme", tak trivialni indukci....)
(existuji spousty zpusobu, jak toto dokazat, napr. kdyz uz vzorec tahto "uhodneme", tak trivialni indukci....)
Proto 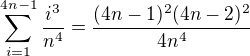 .
.
Podíl polynomů stupně 4, vedoucí koeficient v čitateli 256, ve jmenovateli 4, výsledek 64.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita integrálního součtu (TOTO TÉMA JE VYŘEŠENÉ)


