Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dif. rovnice prvniho radu s PP (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 01. 2011 13:47 — Editoval Crusad (14. 01. 2011 14:18)
dif. rovnice prvniho radu s PP
zdravím, mam problem s cauchyho ulohami. Umim si je celkem obstojne odseparovat, zintegrovat a dostanu pak obecne reseni. Dosadim pocatecni podminky a vyjde mi c. Ale napr. u tohoto prikladu mam problemy, vysledek mi vysel  . V a) nevim odkud se bere ten interval, jinak mi vysledek vysel(c=0). V b) mi vyjde c=-2 a tak mi neni jasny, proc je ve vysledkach to co tam je. A v c) mi vyjde c=4, takze proc tam je ten vysledek a ten interval mi taky unika. Pokud by mi to nekdo vysvetlil, byl bych vdecny.
. V a) nevim odkud se bere ten interval, jinak mi vysledek vysel(c=0). V b) mi vyjde c=-2 a tak mi neni jasny, proc je ve vysledkach to co tam je. A v c) mi vyjde c=4, takze proc tam je ten vysledek a ten interval mi taky unika. Pokud by mi to nekdo vysvetlil, byl bych vdecny.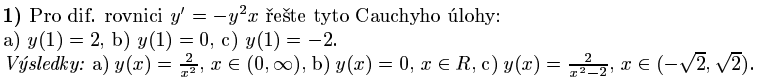
Offline
- (téma jako vyřešené označil(a) Crusad)
#2 14. 01. 2011 15:07 — Editoval maly_kaja_hajnejch-Lazov (14. 01. 2011 15:08)
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: dif. rovnice prvniho radu s PP
Mate ten vysledek spatne.  neni obecne reseni.
neni obecne reseni.
interval: vezme se co nejdelsi interval, ktery je podmnozinou definicniho oboru a obsahuje pocatecni podminku.
Offline
#4 14. 01. 2011 15:40
Re: dif. rovnice prvniho radu s PP
Ten výsledek v b) je podle věty o jednoznačnosti řešení: že bodem [1, 0] prochází graf funkce y(x) = 0, která vyhovuje i té dif. rovnici, je zřejmé.
Ad c: Při separaci proměnných je výhodné pracovat s určitými integrály při využití počáteční podmínky.
Separovanou rovnici  integrujeme na
integrujeme na
 ,
,
odtud po substituci na levé straně obdržíme
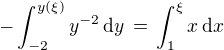 .
.
Výsledek mi vyšel stejně jako v těch materiálech.
Difer. rovnici řešíme na intervalu, v bodech  je definiční obor fce y přerušen.
je definiční obor fce y přerušen.
Offline
#7 14. 01. 2011 16:09
Re: dif. rovnice prvniho radu s PP
↑ Crusad:
Mělo by to být písmeno xi dočasně v roli nové proměnné místo x, když podle x integrujeme (a tudíž ho nemůžeme současně mít
v horní ani v dolní mezi). Až integrály vypočítáme, samozřejmě můžeme za xi dosadit zpátky x.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dif. rovnice prvniho radu s PP (TOTO TÉMA JE VYŘEŠENÉ)

 Tak jsem si to otocil, a nejak jsem zapomnel na c. Takze asi spis
Tak jsem si to otocil, a nejak jsem zapomnel na c. Takze asi spis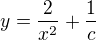 ?
? .
.