Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riemannův integral - výpočet z definice (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 01. 2011 18:37
Riemannův integral - výpočet z definice
Ahoj,
tak to sem zkusim dat jeste jednou (omlouvam se za mnozeni stejnych prispevku - ale doufam, ze se preci jen nekdo najde . . ).
Potřebuji pomoc s tímto příkladem:
Spočtěte použitím definice Riemannova integrálu 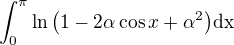 .
.
Pro začátek mám napsaný vzorec pro dolní R. součet , kde dělení D mám jako rovnoměrné dělení intervalu
, kde dělení D mám jako rovnoměrné dělení intervalu  .
.
Nevím jestli už se zvolením jednoho speciálního dělení nedopouštím chyby - totiž vše by mělo být definováno pro všechna dělení . . .
Dále neumím sečíst tuto řadu (at pro konecne n, nebo pak v limitnim pripade pro  ) - po nakreslení v gnuplotu mi dokonce přijde, že diverguje - což je divné. . .
) - po nakreslení v gnuplotu mi dokonce přijde, že diverguje - což je divné. . .
Díky za každou radu (nechci po nikom cele reseni - staci jen nakopnout . . .) .
pi = 3
Offline
- (téma jako vyřešené označil(a) Azeret)
#2 15. 01. 2011 22:16 — Editoval Pavel (15. 01. 2011 22:17)
Re: Riemannův integral - výpočet z definice
↑ Azeret:
Ta úloha je dost nejasná. Co je vůbec  ? Např. když
? Např. když  , tak Riemannův integrál na intervalu
, tak Riemannův integrál na intervalu  nebude existovat. Riemannův integrál je totiž definován pro omezené funkce a funkce
nebude existovat. Riemannův integrál je totiž definován pro omezené funkce a funkce 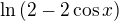 určitě omezená v okolí 0 není. Nemá tedy smysl konstruovat nějaké horní resp. dolní součty.
určitě omezená v okolí 0 není. Nemá tedy smysl konstruovat nějaké horní resp. dolní součty.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 15. 01. 2011 22:32
Re: Riemannův integral - výpočet z definice
↑ Azeret:
I v tomto případě problém zůstává, je-li totiž  , pak funkce
, pak funkce 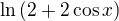 je neomezená v okolí
je neomezená v okolí 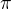 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 16. 01. 2011 00:10
Re: Riemannův integral - výpočet z definice
↑ Azeret:
Po dlouhem premysleni o Riemannove integralu by mi stacilo, kdyby me nekdo nakopl se souctem te rady. Vzhledem k tomu, ze ta funkce je spojita a omezena, tak je riemanovsky integrovatelna a tedy staci spocitat bud horni nebo dolni soucet.
Coz je doufam tohle . . .
. . .
pi = 3
Offline
#7 16. 01. 2011 01:44 — Editoval Pavel (16. 01. 2011 03:16)
Re: Riemannův integral - výpočet z definice
S podobným integrálem jsem se setkal už zde
http://forum.matweb.cz/viewtopic.php?id=17709
Zde je integrál obecnější a jeho výpočet má využívat definici Riemannova integrálu. Až do této chvíle jsem myslel, že toto vypočítat jen tak jednoduše nepůjde.
Nicméně se zadařilo. Bylo sice nutné sáhnout do komplexní analýzy, ale šlo to.
Vzhledem k pokoročílé hodině uvedu postup zítra
Výsledek je však .
.
Můžu se zeptat, odkud máš ten příklad?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 16. 01. 2011 09:49 — Editoval Azeret (16. 01. 2011 10:03)
Re: Riemannův integral - výpočet z definice
↑ Pavel:
Jsem v prvaku na fyzice a tohle jeden z doporucenych prikladu na cviceni ....(http://www.karlin.mff.cuni.cz/~pokorny/cvic1z14.pdf)
Na ten odkaz se podivam, diky moc.
pi = 3
Offline
#9 19. 01. 2011 14:12 — Editoval Pavel (26. 04. 2017 12:16)
Re: Riemannův integral - výpočet z definice
↑ Azeret:↑ Azeret:
Konečně jsem se dostal ke slibovanému řešení:
Riemannův integrál se zavádí pomocí horních a dolních součtů. Nicméně pokud Riemannův integrál funkce  na
na  existuje, mohu jej vypočítat jednodušeji, a to pomocí limity součtů
existuje, mohu jej vypočítat jednodušeji, a to pomocí limity součtů 
pro 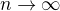 , kde body
, kde body 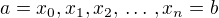 jsou body nějakého dělení intervalu
jsou body nějakého dělení intervalu  takové, že norma tohoto dělení se blíží k 0 pro
takové, že norma tohoto dělení se blíží k 0 pro 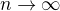 . Místo abych hledal suprema resp. infima funkce
. Místo abych hledal suprema resp. infima funkce  na jednotlivých intervalech
na jednotlivých intervalech 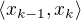 ,
, 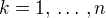 , budu pracovat s jejími funkčními hodnotami v pravých krajních bodech těchto intervalů. Takto lze však Riemannův integrál vypočítat pouze tehdy, je-li zaručena jeho existence.
, budu pracovat s jejími funkčními hodnotami v pravých krajních bodech těchto intervalů. Takto lze však Riemannův integrál vypočítat pouze tehdy, je-li zaručena jeho existence.
Nechť nejdříve 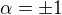 . Pak bylo v předchozích příspěvcích ukázáno, že integrovaná funkce není na intervalu
. Pak bylo v předchozích příspěvcích ukázáno, že integrovaná funkce není na intervalu  omezená a tudíž Riemannův integrál pro tato
omezená a tudíž Riemannův integrál pro tato  neexistuje. Nechť nyní
neexistuje. Nechť nyní 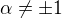 . Pak funkce
. Pak funkce  je na intervalu
je na intervalu  spojitá, omezená a kladná, a proto je také funkce
spojitá, omezená a kladná, a proto je také funkce 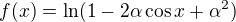 na intervalu
na intervalu  spojitá a omezená (kladná již být nemusí). Pak odsud vyplývá, že hledaný Riemannův integrál opravdu existuje a můžeme jej určit výše zmíněnou technikou:
spojitá a omezená (kladná již být nemusí). Pak odsud vyplývá, že hledaný Riemannův integrál opravdu existuje a můžeme jej určit výše zmíněnou technikou:
------------------------------------------
1. Zvolme nejdříve ekvidistantní dělení intervalu  na
na 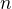 stejných částí, kde
stejných částí, kde 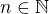 . Dělicími body t tomto dělení jsou body
. Dělicími body t tomto dělení jsou body  .
.
Označme symbolem  sumu
sumu
2. Upravme nejdříve výraz v závorce za součinem
3. Nyní využijme prostředků komplexní analýzy, označme 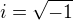 a použijme vzorec
a použijme vzorec 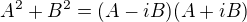 .
.
4. Nahraďme goniometrický tvar komplexního čísla tvarem exponenciálním, tzn. 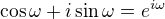 ,
, 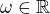 , a využijme toho, že platí
, a využijme toho, že platí 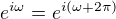 .
.
5. Vraťme se nyní k původnímu součinu. Platí tedy, že![kopírovat do textarea $ \prod_{k=1}^n\left(1-2\alpha\cos\frac{k\pi}{n}+\alpha^2\right)=\prod_{k=1}^n\left(1-\alpha e^{\frac{k\pi}{n}i}\right)\left(1-\alpha e^{\frac{(2n-k)\pi}{n}i}\right)=\nl =\left(1-\alpha e^{\frac{\pi}{n}i}\right)\left(1-\alpha e^{\frac{(2n-1)\pi}{n}i}\right)\left(1-\alpha e^{\frac{2\pi}{n}i}\right)\left(1-\alpha e^{\frac{(2n-2)\pi}{n}i}\right)\cdots\nl \cdots\left(1-\alpha e^{\frac{(n-1)\pi}{n}i}\right)\left(1-\alpha e^{\frac{(n+1)\pi}{n}i}\right)\left(1-\alpha e^{\frac{n\pi}{n}i}\right)\left(1-\alpha e^{\frac{n\pi}{n}i}\right)=\nl =\left[\left(1-\alpha e^{\frac{\pi}{n}i}\right)\left(1-\alpha e^{\frac{2\pi}{n}i}\right)\cdots\right.\nl \left.\cdots\left(1-\alpha e^{\frac{(n-1)\pi}{n}i}\right)\left(1-\alpha e^{\frac{n\pi}{n}i}\right)\left(1-\alpha e^{\frac{(n+1)\pi}{n}i}\right)\cdots \left(1-\alpha e^{\frac{(2n-2)\pi}{n}i}\right)\left(1-\alpha e^{\frac{(2n-1)\pi}{n}i}\right)\right]\cdot \left(1-\alpha e^{\frac{n\pi}{n}i}\right) $](/mathtex/ec/ec4e1f61871a58aa6051bf7d2198cbf9.gif)
6. Prozkoumáme-li pozorněji na výrazy ve všech závorkách, pak komplexní členy uvnitř jsou ve skutečnosti kořeny speciální binomické rovnice. jsou všechny kořeny binomické rovnice
jsou všechny kořeny binomické rovnice 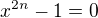 v komplexním tvaru.
v komplexním tvaru. jsou všechny kořeny binomické rovnice
jsou všechny kořeny binomické rovnice 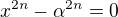 v komplexním tvaru.
v komplexním tvaru.
Známe-li kořeny algebraické rovnice 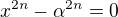 , můžeme vyjádřit polynom
, můžeme vyjádřit polynom 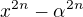 pomocí součinu svých kořenových činitelů. Tj.
pomocí součinu svých kořenových činitelů. Tj.
Nyní dosaďme  ,
,
7. Všimněme si, že tento součin je téměř stejný jako součin, který jsme upravovali na konci bodu č. 5. Zde nadbývá výraz, který je mimo hranatou závorku a chybí výraz 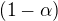 , který se vyskytuje v součinovém vyjádření
, který se vyskytuje v součinovém vyjádření 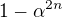 .
.
Proto platí
8. Nyní můžeme vypočítat integrál jako 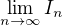 :
:
a) Nechť  . Pak
. Pak
b) Nechť nyní  . Pak
. Pak 
Tzn.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Riemannův integral - výpočet z definice (TOTO TÉMA JE VYŘEŠENÉ)

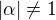 , jinak
, jinak  . . .ted uz snad vse ok. .
. . .ted uz snad vse ok. .