Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 04. 2008 00:31 — Editoval Kondr (30. 04. 2008 16:43)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Užitečné vzorce
Budiž zde dána jednoduchá "kuchařka" na úpravu vzorců, na kterou bude možno odkazovat. Časem ji trochu rozšířím a bude-li čas, přemístím ji mimo fórum, aby bylo možno přes kotvy odkazovat na jednotlivé vzorce.
V následujícím textu je n číslo přirozené, ztímco a,b mohou být čísla libovolná (reálná, komplexní, z okruhu 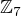 ,... )
,... )
#
(1.1) 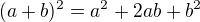
#
(1.2) 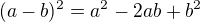
#
(1.3) 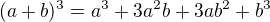
#
(1.4) 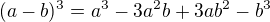
#
(1.5) 
#
(1.6) 
(vznikne z 1.5 náhradou b za -b; to se projeví změnou znamének sčítanců na sudých pozicích zleva)
#
(2.1) 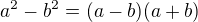
#
(2.2) 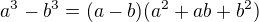
#
(2.3) 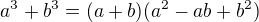
#
(2.4) 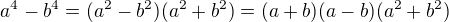
#
(2.5) 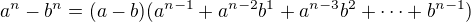
#
(2.6) Pro lichá k: 
#
(2.7) Pro sudá k: 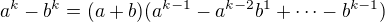
#
(2.8) 
Následujíc vzorce platí pro kladné p a libovolná a,b; pro záporné p platí jen pro a,b přirozená (případně racionální s lichým jmenovatelem). Pokud se pohybujeme v komplexních číslech, pak p může být libovolné komplexní číslo a a,b libovolná reálná (o rozšíření na komplexní a,b je předpokládám zbytečné psát).
#
(3.1)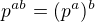
#
(3.2)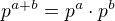
#
(3.3)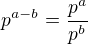
#
(3.4)![kopírovat do textarea $p^{\frac{a}n}=\sqrt[n]p^a}$](/mathtex/50/50e5c92b7ce8b8689f4986a0accb6cbe.gif)
#
(4.1)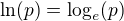
#
(4.2)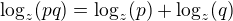
#
(4.3)
#
(4.4)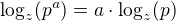
#
(4.5)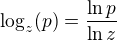
#
(5.1)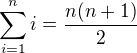
#
(5.2)
#
(5.3)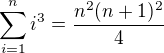
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#2 30. 04. 2008 00:35
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Užitečné vzorce
A kdybyste to chtěli někdo někde odkazovat, tak http://navzorce.jdem.cz
BRKOS - matematický korespondenční seminář pro střední školy
Offline