Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#6 29. 01. 2011 10:02 — Editoval FailED (29. 01. 2011 10:16)
Re: Limita posloupnosti
↑ Crusad:
NE! Máš limitu 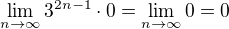 .
.
Stejně tak limita 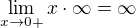 . Nebo
. Nebo  .
.
Limita v bodě vůbec nic nevypovídá o hodnotě výrazu v tom bodě (nebo jeho definovanosti), zajímá nás jen prstencové okolí, kdyby šlo o hodnotu v bodě, nemělo by smysl limity vůbec zavádět.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)

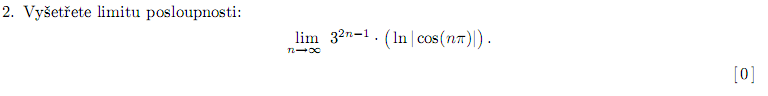
 má limitu nevlastní a vyjde
má limitu nevlastní a vyjde 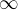 . Problém ale mám, s tím logaritmem. Ten limitu v
. Problém ale mám, s tím logaritmem. Ten limitu v  nemá. Co pak s tím logaritmem? Výsledek má vyjít nula. Jak se k tomu dostat?
nemá. Co pak s tím logaritmem? Výsledek má vyjít nula. Jak se k tomu dostat? je konstanta...
je konstanta... .
.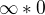 . To bych si měl asi přepsat na
. To bych si měl asi přepsat na  a použít l'Hospitala?
a použít l'Hospitala? a zderivovat?
a zderivovat?