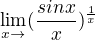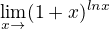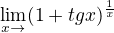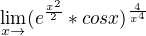Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 05. 2008 15:41
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Limitky
Přístup (1+0)^ln0=(1+0)^1=1 nefunguje, protože logaritmus nuly je -oo. Musí se použít vztah ,
,
pak pomůže L'Hospital.
Ve druhém a třetím příkladě jde použít trik s eulerovým číslem, ukážu to na tom druhém: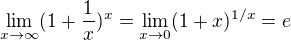
![kopírovat do textarea $\lim_{x\to 0} (1+x)^{\ln x}=\lim_{x\to 0} [(1+x)^{1/x}]^{x\ln x}=\lim_{x\to 0} e^{x\ln x}=e^0=1$](/mathtex/e4/e4574b442bca67c8b21e3de375bedd1b.gif)
(proč jde x lnx k nule není zřejmé, ale už je to opět standardní L'Hospital.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 02. 05. 2008 20:38
Re: Limitky
↑ nika.v: Jen dodám, že  je nedefinovaný výraz, proto nemůžeš udělat úpravu, kterou jsi naznačila u druhého příkladu
je nedefinovaný výraz, proto nemůžeš udělat úpravu, kterou jsi naznačila u druhého příkladu
(viz např. http://www.fsid.cvut.cz/cz/U201/map/mat … app201.htm)
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#4 05. 05. 2008 10:55
Re: Limitky
↑ Kondr:
No, to jsi moc nepomohl. Mě ty limity nejdou do hlavy. Písnu moje pokusy a úvahy, mrkneš se na ně?
U prvního příkladu vím, že lim, když x jde k 0 argumentu sinx/x je pravidlem = 1, ovšem mrší mi to tu 1/x, ale zase 1 na cokoliv je vždy 1 a při použití l´Hospitala mi vyjde hrůza.
U příkladu s (1+tg x) na 1/x, když použiji l´Hospitala, tak se nikam nedostanu a upravit to na výraz (1+x)na1/x fakt neumím.
Poslední příklad s (ena (xna2/2) * cosx)na (4/xna4), tak na tento příklad koukám cca 14 dní a nic jsem nevymyslela. Když zkusím l´Hospitala zase mi vyjde hrůza.
Offline
#5 05. 05. 2008 11:23 — Editoval Jorica (05. 05. 2008 14:09)
Re: Limitky
↑ nika.v:
urcite budes muset postupovat podle vztahu, co ti tu navrhl ↑ Kondr:, a to:
Neni totiz pravda, ze 1 na cokoliv je 1...prave  je neurcity vyraz, pokud pouzijes vyse uvedeny vztah, prevedes limitu na tvar nula lomeno nulou a pouzijes l'Hospitala...zkusim naznacit:
je neurcity vyraz, pokud pouzijes vyse uvedeny vztah, prevedes limitu na tvar nula lomeno nulou a pouzijes l'Hospitala...zkusim naznacit: , kde
, kde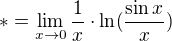
Pokud vyraz za limitou zapises takto: , dostavas po dosazeni nuly neurcity vyraz nula lomeno nulou a pouzijes l'Hospitala...nekolikrat za sebou, az se dopracujes k vyseldku....a ten pak dosadis do exponentu cisla e (misto *) a mas hodnotu vysledne limity.
, dostavas po dosazeni nuly neurcity vyraz nula lomeno nulou a pouzijes l'Hospitala...nekolikrat za sebou, az se dopracujes k vyseldku....a ten pak dosadis do exponentu cisla e (misto *) a mas hodnotu vysledne limity.
Editace: tak mi po 3 l'Hospitalech vysla samotna limita rovna 0 a po dosazeni do exponentu je vysledek zadane limity 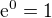 ...tak snad tam neni chyba ;)
...tak snad tam neni chyba ;)
Ostatni priklady bys mela pocitat obdobne.
Offline
#8 05. 05. 2008 13:00 — Editoval nika.v (05. 05. 2008 13:09)
Re: Limitky
U prvního příkladu jsem zkusila toto: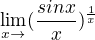 = l´Hospital
= l´Hospital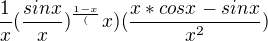
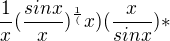
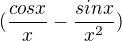
No, ale teď babo raď. To mám stále pokračovat s l´Hospitalem? Po pravdě ani nevím jak, protože umím (fg)´, ale (abcd)´ to fakt neumím
a mimochodem, když si tyto zápisy frknu do texu, tak je to v pohodě a jak je lupnu sem, tak mi to v náhledu ukazuje chyby, to jsem z toho jelenec
Offline
#9 05. 05. 2008 14:05 — Editoval Jorica (05. 05. 2008 14:10)
Re: Limitky
↑ nika.v:
Z toho zapisu nejsem moc moudra, jak jsi to derivovala :( koukni na ten muj postup a vyslednou limitu  (aby sel pouzit l'Hospital, musi to byt podil a po dosazeni musi vychazet 0/0 nebo oo/oo), coz ta moje limita splnuje...u te tve to nedokazu posoudit, ten zacatek se mi nezobrazuje...ted derivuj zvlast citatele (jako slozenou fci) a zvlast jmenovatela ....pokud budes pouzivat l'Hospitala nekolikrat, porad musis mit za limitou podil 0/0 nebo oo/oo.
(aby sel pouzit l'Hospital, musi to byt podil a po dosazeni musi vychazet 0/0 nebo oo/oo), coz ta moje limita splnuje...u te tve to nedokazu posoudit, ten zacatek se mi nezobrazuje...ted derivuj zvlast citatele (jako slozenou fci) a zvlast jmenovatela ....pokud budes pouzivat l'Hospitala nekolikrat, porad musis mit za limitou podil 0/0 nebo oo/oo.
Natukam ti dalsi kousek z te 1...ostatni priklady jsou totez dokola, nekde jsem tu na smiraku pocitala i tu posledni limitu a vyslo mi snad 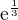 ...ted to nemuzu najit, ale postup byl stejny...tak k te 1:
...ted to nemuzu najit, ale postup byl stejny...tak k te 1:
 l'Hospital
l'Hospital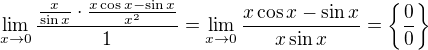 l'Hospital
l'Hospital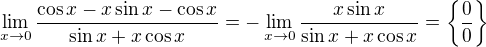 l'Hospital
l'Hospital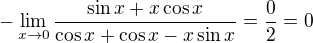
No a kdyz nulu vratim do exponentu, vyjde, jak uz jsem psala 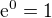
Podrobneji uz to rozepsat neumim, je tam kazdy krok, samo, ze derivuji citatele a jmenovatele zvlast, jen jsou tam souciny, takze uvazit derivaci soucinu. Za preklepy se omlouvam, tukam to tu se synem na kline a porad se mi snazi opravovat chyby :)
Offline