Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 05. 2008 21:10
- petulkacip
- Příspěvky: 38
- Reputace: 0
goniometrie
DEKUJU MOC, ted se snazim prijit na dalsi priklad..dokonce jsem si i namalovala graf, ale porad mi to nevychazi podle vysledku....
vsechna x nalezi do <0; 2pi>, ktera splnuji podminku |cos x/2| < nebo rovno 1/2 tvori mnozinu
prosim pekne o postup....
Offline
#3 06. 05. 2008 21:35
Re: goniometrie
v tomto pripade plati, ze obrazek je celkem uzitecny k vyreseni. staci si uvedomit, ze vzdalenost bodu 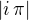 je stejna jako vzdalenost bodu
je stejna jako vzdalenost bodu 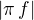 , staci tedy spocitat bod
, staci tedy spocitat bod  z rovnice
z rovnice  , dopocitat symetricky bod
, dopocitat symetricky bod  a jak je videt z obrazku, resenim je interval
a jak je videt z obrazku, resenim je interval 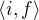
Offline
#4 06. 05. 2008 21:38
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
↑ plisna: ouou, neslo by to malinko vice polopate? PROSIM
Offline
#5 06. 05. 2008 21:41
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
↑ plisna: musi se to pocitat pres to i??? to je na me nejake slozite, neni tam jednodussi cesta k vyledku?? ve vysledkach mi totiz napsali ze to je = <2pi / 3; 4pi / 3>
Offline
#7 06. 05. 2008 21:54
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
↑ plisna: pro jaky bod? promin, me to moc matematicky nemysli, ale potrebuju s tim pomoct...:(
Offline
#9 06. 05. 2008 22:04
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
↑ plisna:no jo, ale jakou ma hodnotu? promin, tohle asi nema cenu... ale dekuju za snahu!!!!!!:)
Offline
#11 06. 05. 2008 22:19 — Editoval petulkacip (06. 05. 2008 22:20)
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
↑ plisna: dekuju! me to stejne nejak nejde... ale moc dekuju za snahu!!!
Offline
.png)

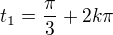 a
a 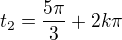 . vratime se zpet k substituci a mame
. vratime se zpet k substituci a mame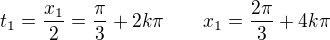
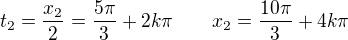
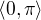 je koren
je koren 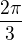 , coz je hledane cislo
, coz je hledane cislo