Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 09. 05. 2008 13:50 — Editoval robert.marik (09. 05. 2008 13:50)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: extrémy
v bode ![kopírovat do textarea $[x_0,y_0] $](/mathtex/c5/c5712ed5395426a020bd5250f5659490.gif) se musi sestrojit tecna, pak se musi najit pruseciky tecny s osami a vypocitat ten obsah. Vyjde treba obsah jako funkce promenne x_0
se musi sestrojit tecna, pak se musi najit pruseciky tecny s osami a vypocitat ten obsah. Vyjde treba obsah jako funkce promenne x_0
A potom je to klasicka uloha na extremy funkce jedne promenne
Staci takove natuknuti?
Offline
#4 09. 05. 2008 14:05
Re: extrémy
↑ rasky22:
Robert me predbehl, nez jsem si nacmarala obrazek. 
Souhlas s nim. Nezarucim, ze to mam spocteno dobre, pracuji na necem jinam a tak jsem se na to moc nesoustredila, ale z rovnice tecny jsem si nasla pruseciky s osami....jsou vyznaceny v obrazku. Ted bych do rovnice elipsy dosadila misto x x_0 a vypocitala dve hodnoty y_0 (lisi se ve znamenku +-, proto jsou v obrazku zaznaceny dva body dotyku tecny). Tim budes mit obe strany trojuhelnika vyjadrene jen pomoci jedne nezname x_0.
Zapises vztah pro obsah trojuhelnika, ten podle x_0 derivujes a hledas extrem. Tak jen doufam, ze tato cesta vede k cili ;-)
Offline
#7 09. 05. 2008 20:49
Re: extrémy
↑ rasky22:
Vychazim z obrazku vyse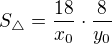
Do rce elipsy dosadim x_0 a vyjadrim y_0 nasledovne: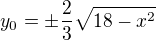
Plochu trojuhelnika diky tomu vyjadrim jen pomoci jedne promenne x_0:
Tohle derivuji podle x_0 (zkus, jestli se dopocitas taky, kdyztak to rozepisu):
Plati, ze  . Odtud mas dve reseni
. Odtud mas dve reseni 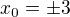
Dosazenim zpet mas ke kazdemu x_0 dve reseni pro y_0, takze celkem 4 body dotyku (coz se diky symetrii elipsy dalo cekat).
Offline
#9 09. 05. 2008 21:08 — Editoval robert.marik (09. 05. 2008 21:11)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: extrémy
↑ Jorica:
klobouk dolů, já jsem neměl čas topočítat. přidal bych ale malý trik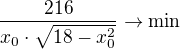
je ekvivalentní problému  a to je pro kladná přípustná x_0 ekvivalentní problému
a to je pro kladná přípustná x_0 ekvivalentní problému 
Takže líní derivují funkci  ;)
;)
a ti úplně nejlínější ani nederivují, ale malují parabolu 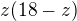 , hledají její vrchol (uprostřed mezi kořeny) a odmocňují x-ovou souřadnici kořene
, hledají její vrchol (uprostřed mezi kořeny) a odmocňují x-ovou souřadnici kořene
Offline
#10 09. 05. 2008 21:11 — Editoval Jorica (09. 05. 2008 21:11)
Re: extrémy
↑ robert.marik:
Hele, a to pises az ted, kdyz jsem to zderivovala? :-) Jinak zdravim ;-)
Ale diky, ze me nepovazujes za linou....jen mozna za natvrdlou :-))))
Offline
#11 09. 05. 2008 21:12
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: extrémy
↑ Jorica:
nojo, když já jsem fakt neměl čas :) Ahoj. R.
Offline
#12 09. 05. 2008 21:13
Re: extrémy
↑ robert.marik:
Ahoj, no jo, tak snad priste prijdu z prace jeste pozdeji nez dnes a budes rychlejsi :-)
Offline
#14 09. 05. 2008 21:20
Re: extrémy
↑ rasky22:
No vidis, davas pozor :-))) jasan, ze je, ale na derivaci to nastesti nema vliv ;-) Ale dopis si tam tu polovinu.
Offline
#18 09. 05. 2008 23:57
#19 10. 05. 2008 00:25
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: extrémy
↑ rasky22:
ani se nedivím, já jsem to ručně nepočítal (lenost)
v limitních polohách  a
a  funkce "uteče do nekonečna" a všude mezi tím je hladká a nabývá nějakých reálných hodnot. Logicky tam tedy někde musí být minimum. A protože stacionární bod an tomto intervalu je jenom x=3, musí to minimum být právě tam. Druhou derivaci v praktických úlohách většinou vůbec nepotřebujeme, protože to, že to je ten správný druh extrému, většinou vyplývá "z logiky věci".
funkce "uteče do nekonečna" a všude mezi tím je hladká a nabývá nějakých reálných hodnot. Logicky tam tedy někde musí být minimum. A protože stacionární bod an tomto intervalu je jenom x=3, musí to minimum být právě tam. Druhou derivaci v praktických úlohách většinou vůbec nepotřebujeme, protože to, že to je ten správný druh extrému, většinou vyplývá "z logiky věci".
Offline
#20 13. 05. 2008 22:18
Re: extrémy
↑ rasky22:
Taky mám problém s tímto příkladem. Pořád si nejsem jistý jak vypadá konečný výsledek. Mohl by to prosím někdo rozepsat.
Offline
#23 14. 04. 2009 17:45
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: extrémy
asi je potreba napsat tu rovnici tecny a vypocitat to.
pri psani te tecny se da vyuzit bud diferencialni pocet jako u kazde jine funkce, nebo (pokud umite) analyticka geometrie kuzelosecek.
Offline
#25 14. 04. 2009 20:40
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: extrémy
klicova slova elipsa a polara vedou v googlu treba na tohle:
http://maths.cz/clanky/analyticka-geome … rimka.html
Offline