Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Existence prvku prvočíselného řádu (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 03. 2011 08:23
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Existence prvku prvočíselného řádu
Dokažte, že pokud prvočíslo p dělí řád grupy G, existuje g z G, že g je řádu p.
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) check_drummer)
#2 20. 03. 2011 10:42
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Existence prvku prvočíselného řádu
↑ check_drummer:
Můžu se jen zeptat, jestli znáš nějaký relativně jednoduchý důkaz? Protože ty, které jsem našel na internetu, bych asi nevymyslel.
Offline
#3 20. 03. 2011 13:51
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: Existence prvku prvočíselného řádu
↑ Pavel Brožek:
Abych řekl pravdu, nenašel. Jen jsem teď četl článek, který tvrdil, že by to mělo být důsledkem tvrzení, že řád podgrupy dělí řád grupy. Ale nějaký přímý důsledek jsem neobjevil...
"Máte úhel beta." "No to nemám."
Offline
#4 29. 03. 2011 10:03
Re: Existence prvku prvočíselného řádu
Já bych to viděl takto:
Obecně (v ne nutně komutativním světě) uvážit 1. Sylowovu větu, která zaručuje existenci alespoň jedné p-podgrupy. Skoro mám pocit, že tady nastolená otázka je vlastně jen přeformulací 1. Sylowovy věty (ona má ještě benefit v podobě jakéhosi vyčíslení "kp+1" počtu těch podgrup).
Máme-li p-podgrupu, prvky v ní mají řád mocniny p, takže vhodná mocnina každého prvku z p-podgrupy je prvek řádu p.
V komutativním světě, pokud by to stačilo, máme větu o klasifikaci konečných komutativních grup (až na izomorfismus je každá vhodným součinem mocnin grup 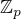 ), odkud je hledaný prvek vlastně hned vidět (až na jednu
), odkud je hledaný prvek vlastně hned vidět (až na jednu 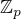 , kde beru její generátor, beru všude jinde jedničky).
, kde beru její generátor, beru všude jinde jedničky).
Offline
#5 29. 03. 2011 10:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Existence prvku prvočíselného řádu
↑ musixx:
Já jsem právě narazil při hledání na Cauchy's theorem (který říká přesně to, co máme dokázat), kde ty důkazy nevypadaly jednoduše, proto jsem se ptal. Tam Sylowovu větu také zmiňují.
Offline
#6 29. 03. 2011 19:39
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: Existence prvku prvočíselného řádu
↑ musixx:
Ovšem samotný důkaz těchto vět není zcela zřejmý. Existuje nějaký přímočarý důkaz nastíněné věty? (Obecně pro nekomutativní grupy.)
"Máte úhel beta." "No to nemám."
Offline
#7 30. 03. 2011 07:25
Re: Existence prvku prvočíselného řádu
↑ check_drummer: Docela bych pochyboval, že Sylowovy věty jsou tvrzení, kde by existovaly důkazy na dva řádky s použitím pouze věcí elementárnějších. Bral jsem je vždy jako standardní nástroje pomáhající v práci v nekomutativních grupách, dokonce nevím, byly-li jejich důkazy vůbec konstruktivní. Málokdy si přeci jednoduché přímočaré tvrzení zaslouží jméno...
Kromě toho, Pavlem zmíněná Cauchyho věta je lepší stopa. V mé odpovědi jsem používal jen to, co jsem znal, a to ta věta nebyla. :-) Takže jsem vlastně původní otázku odpověděl poměrně snadno, s použitím naprosto standardního nástroje, bohužel ale nástroje silnějšího než je vlastní otázka -- i když to teda nebylo přímo "s kanónem na vrabce" (což by podle mě bylo, kdybych se na Sylowovy věty odvolával v případě grupy S_3).
Offline
#8 31. 03. 2011 16:48
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: Existence prvku prvočíselného řádu
↑ musixx:
Pod "větou" jsem měl na mysli právě Cauchyovu větu, nikoli Sylowovy.
"Máte úhel beta." "No to nemám."
Offline
#9 01. 10. 2011 12:14
Re: Existence prvku prvočíselného řádu
ahoj check_
Pozri sa na stranu 119 v American Mathematical Monthly, vol.066 (1959) a precitaj si zajimavu mathematical nate od James H. McKay
srdecne
vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 14. 04. 2012 08:30 — Editoval OiBobik (19. 04. 2012 21:17)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Existence prvku prvočíselného řádu
↑ check_drummer:
Já to znám přes akci grupy na množině. Nevím, jestli je to dost přímočaré, ale určitě je to celkem hezký důkaz.
Tj. toto:
EDIT: Jde o stejný důkaz, jako v článku, na nějž odkazuje ↑ vanok:. (Nevěděl jsem to.)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#11 16. 04. 2012 20:32
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: Existence prvku prvočíselného řádu
↑ OiBobik:
Ahoj, velmi pěkný důkaz.
"Máte úhel beta." "No to nemám."
Offline
#12 17. 04. 2012 01:27 — Editoval vanok (20. 04. 2012 14:16)
Re: Existence prvku prvočíselného řádu
↑ OiBobik:
Ahoj si si nevsimol, referencie clanku o ktorom som pisal trochu vyssie ↑ vanok: . Ide v nom vlastne o prvy znamy dokaz, uplne isty ako ten tvoj.
To iste pomoze kolegom, ze maju prelozenu dokonalu verziu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 19. 04. 2012 00:00
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Existence prvku prvočíselného řádu
↑ vanok:
Ahoj,
promiň, toho tvého odkazu jsem si nevšiml. Jen jsem prohlédl zadání a zběžně jsem viděl, že tu zatím není napsáno žádné řešení, tak jsem napsal důkaz, který znám.
To je mi líto, že jsem tě opět něčím popudil. Pokud ti na tom záleží, můžu ten důkaz smazat.
A ne, opravdu jsem ten důkaz nepřekládal z toho článku, jak naznačuješ.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#14 19. 04. 2012 14:49
Re: Existence prvku prvočíselného řádu
↑ OiBobik:
Ahoj,
Vsak sme to dali na jasno vdaka konstruktivnemu dialogu, a ani ja som ta v ziadnom pripade nechcel urazit, ale ten dokaz, co som citoval je ako sa zda prvy dokaz tohto typu.
Inac by bolo zaujimave, najst v literature, historicky vyvin dokazov tejto vety ( ktorej autor je pravdepodobne Cauchy).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Existence prvku prvočíselného řádu (TOTO TÉMA JE VYŘEŠENÉ)
 je konečná grupa,
je konečná grupa,  prvočíslo takové, že
prvočíslo takové, že  .
.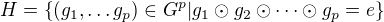
 (kdykoli zvolím prvních (p-1) prvků
(kdykoli zvolím prvních (p-1) prvků  , existuje právě jeden prvek, jak p-tici doplnit tak, aby náležela do
, existuje právě jeden prvek, jak p-tici doplnit tak, aby náležela do  , a sice prvkem
, a sice prvkem 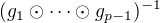 ). Tedy speciálně
). Tedy speciálně  .
.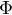 grupy
grupy 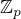 na
na  (tj. "cyklické přetočení o k pozic jedním směrem"). Je jasné, že je to zobrazení na
(tj. "cyklické přetočení o k pozic jedním směrem"). Je jasné, že je to zobrazení na 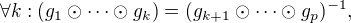 tedy tyto prvky komutují) a že je to skutečně akce na
tedy tyto prvky komutují) a že je to skutečně akce na 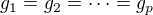 ), nebo p-prvkové (kdykoli jindy).
), nebo p-prvkové (kdykoli jindy). počet jednoprvkových orbit a
počet jednoprvkových orbit a  počet p-prvkových orbit. pak je jasné, že
počet p-prvkových orbit. pak je jasné, že 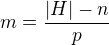 . Jelikož však
. Jelikož však  . Zároveň
. Zároveň 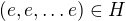 je prvek, který má jednoprvkovou orbitu. Tedy
je prvek, který má jednoprvkovou orbitu. Tedy  a tedy
a tedy  . V grupě tedy existuje prvek
. V grupě tedy existuje prvek 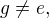 že
že 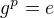 . Vzhledem k tomu, že
. Vzhledem k tomu, že 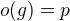 .
.