Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů? (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 03. 2011 00:45 — Editoval claudia (21. 03. 2011 00:46)
Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů?
Dobrý večer,
při řešení úlohy ve vedlejším tématu jsem narazila na problém dokázat, že řada  má omezenou posloupnost částečných součtů (pro následné užití v Dirichletově kritériu). Je to sice na první pohled vidět, ale není mi jasné, jak to korektně dokázat nějakým stručným způsobem.
má omezenou posloupnost částečných součtů (pro následné užití v Dirichletově kritériu). Je to sice na první pohled vidět, ale není mi jasné, jak to korektně dokázat nějakým stručným způsobem.
Uměla bych tvrdit, že posloupnost členů je periodická s periodou 6 a součet prvních šesti členů je roven nule (a zbylých pět částečných součtů je omezených), ale takový argument by bylo prakticky nemožné použít, pokud by v zadání namísto toho bylo např.  .
.
Možná žádný takový způsob neexistuje, ale pokud nějaký znáte, budu za něj ráda.
Děkuji.
Offline
- (téma jako vyřešené označil(a) claudia)
#3 21. 03. 2011 01:04 — Editoval claudia (21. 03. 2011 01:14)
Re: Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů?
↑ Stýv:
Já mám poznámky vedle sebe, ale mám tam důkaz jen pro posloupnost mocnin komplexního čísla s jednotkovou absolutní hodnotou. Napadlo mne, že by to mohlo souviset, ale není mi na první pohled jasné jak.
EDIT: Mohlo by to souviset s omezeností imaginární části nějakého čísla. To číslo zjevně bude  :-) A protože posloupnost částečných součtů n-tých mocnin tohoto čísla je omezená, musí být omezená i jeho imaginární složka, která odpovídá součtům naší řady. Děkuji :-)
:-) A protože posloupnost částečných součtů n-tých mocnin tohoto čísla je omezená, musí být omezená i jeho imaginární složka, která odpovídá součtům naší řady. Děkuji :-)
Ještě nějaké triky k tématu? :-)
Offline
#4 21. 03. 2011 02:16
Re: Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů?
Je to přesně jak říkáš. Eventuálně lze využít vzorec, který je "odvozen" v posledním článku (Ze společenského večera) zde.
Offline
#5 21. 03. 2011 02:55
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů?
Uměl bych tvrdit, že posloupnost členů je periodická s periodou 768 a součet prvních 768 členů je roven nule (a zbylých 767 částečných součtů je omezených).
Stačí mi k tomu  .
.
@Olin: Díky za odkaz. Podpora antitalentů pobavila.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 21. 03. 2011 21:07
Re: Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů?
↑ Olin:
Děkuji :-) Ještě lepší než důkaz byla zmínka o královské cestě :-)
Nicméně původně jsem vůbec nepochopila, že ten vztah opravdu platí :-)
↑ Kondr:
Také děkuji, to by asi bylo dostatečné. Nicméně metody, ke kterým mě přivedli Stýv s Olinem mi přijdou transparentnější a pokrývají větší množství případů (zejm. důležité případy, kdy by se z argumentu vynechalo to pi :-)
Offline
#7 22. 03. 2011 09:13
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů?
↑ claudia:
My jsme se na cvičeních k analýze učili postupovat takto:
Pro x různé od násobků  je pěkně vidět, že to je omezené. Tenhle postup je užitečný, když se vyšetřuje, jestli jsou částečné součty omezeny stejnoměrně (tj. nezávisle na x). Stejnoměrně omezené budou pouze pro
je pěkně vidět, že to je omezené. Tenhle postup je užitečný, když se vyšetřuje, jestli jsou částečné součty omezeny stejnoměrně (tj. nezávisle na x). Stejnoměrně omezené budou pouze pro  , kde
, kde  je nějaké malé kladné číslo. V okolí nuly jsou problémy. (To, že částečné součty rostou nade všechny meze, je dobře vidět, když vezmeme vztah, na který upozornil Olin, volíme
je nějaké malé kladné číslo. V okolí nuly jsou problémy. (To, že částečné součty rostou nade všechny meze, je dobře vidět, když vezmeme vztah, na který upozornil Olin, volíme  a pošleme
a pošleme 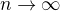 .)
.)
Samozřejmě, ten vztah od Olina je jednodušší použít, ale já si ho třeba nepamatuji. Naopak v tom postupu ode mě je v každém kroku okamžitě jasné, jak pokračovat.
Třeba si na tohle někdy vzpomeneš, až se dostanete ke stejnoměrné konvergenci (pokud už u ní nejste, ale to bych se divil, byli byste rychlejší než fyzici, kteří to neberou tak důkladně) :-).
Pozn.: Stejně lze postupovat i pro kosinus. :-)
Offline
#8 24. 03. 2011 13:26
Re: Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů?
↑ Pavel Brožek:
Děkuji, vypadá to logicky, ale intuitivní to pro mne ještě není :-) Naopak to již mnoho dní vzdoruje mé snaze si to představit :-)
----------------------------------------------------------------------------------------------------
Znovu děkuji všem za nápady.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jak snadno ukázat, že řada má omezenou posloupnost částečných součtů? (TOTO TÉMA JE VYŘEŠENÉ)
