Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 07. 04. 2011 21:35 — Editoval OiBobik (07. 04. 2011 21:36)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ byk7:
Doplnění na rovnoběžník s dvojnásobkem jedné z těžnic jako s diagonálou, využiješ dále toho, že těžiště je ve třetině každé těžnice. taky budeš konstruovat kružnici, ze které "je vidět" na půlku této diagonály se zorným úhlem 
Doplnění na rovnoběžník jsou přesně ty úlohy, proč nemám rád planimetrii : ))
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 07. 04. 2011 22:40 — Editoval BakyX (07. 04. 2011 22:40)
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ OiBobik:
Ono sa to dá aj bez doplnenia na rovnobežník => môžeš začať milovať planimetriu :)
Narysuješ ťažnicu tc. Nájdeš ťažisko. Nájdeš množinu bodov, pod ktorými je ťažnicu tc vidieť pod uhlom alfa. Pomocou kružnice so stredom v ťažisku a polomerom 2/3 tb nájdeš bod A. Bod B potom nie je problém s použitím stredovej súmernosti.
Chceš pomôcť aj s podmienkami ? :)
1^6 - 2^6 + 3^6 = 666
Offline
#4 07. 04. 2011 22:54 — Editoval OiBobik (07. 04. 2011 23:26)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ BakyX:
já předpokládám (podle obvyklých konvencí u trojúhelníka), že  je u vrcholu A a že tb, tc jsou postupně těžnice na strany b,c, nikoli a. Chápeme oba zadání stejně? Přijde mi, že si myslíš, že tb je úsečka s jedním koncem u vrcholu, kde je onen úhel
je u vrcholu A a že tb, tc jsou postupně těžnice na strany b,c, nikoli a. Chápeme oba zadání stejně? Přijde mi, že si myslíš, že tb je úsečka s jedním koncem u vrcholu, kde je onen úhel  .
.
můj postup je vlastně stejný, jako tvůj, akorát A je průnik oné zorné kružnice s kružnicí s poloměrem 2/3 tb, která má ale střed nikoli v těžišti, ale v jeho obrazu středově souměrném podle středu úsečky AB - tedy u mě podle středu onoho doplněného čtyřúhelníku (T' - střed oné kružnice o pol. 2/3tb - je vlastně těžiště onoho "doplněného" trojúhelníka).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 04. 06. 2023 17:14
- Vojtěch Šebek

- Zelenáč
- Příspěvky: 6
- Škola: SPŠE Plzeň
- Pozice: Student, obor IT
- Reputace: 0
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
Zdravím,
velice se omlouvám za znovuotevření tohoto úkolu, ale měl bych otázku k tomuto zadání. Jak mám tento trojúhelník zkonstruovat, když ale musím začít úhlem alfa?
Předem děkuji za jakoukoliv odpověď.
Offline
#6 04. 06. 2023 17:45
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ Vojtěch Šebek:
Ahoj, narýsuj nějam úhel alfa, pak použij konstrukci výše (mimo tento úhel alfa), a nakonec přenes takto sestrojený trojúhelník tak, aby jeho úhel alfa byl totožný s úhlem alfa sestrojeným v prvním kroku.
"Máte úhel beta." "No to nemám."
Offline
#7 04. 06. 2023 18:19 — Editoval Vojtěch Šebek (04. 06. 2023 18:22)
- Vojtěch Šebek

- Zelenáč
- Příspěvky: 6
- Škola: SPŠE Plzeň
- Pozice: Student, obor IT
- Reputace: 0
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ check_drummer:
Takže jestli jsem to pochopil správně tam mám normálně začít těžnicí (b nebo c) a pak výsledný trojúhelník nanést na původní úhel alfa?
A ještě jedna otázka, podmínky pro tuto konstrukci náhodou nevíte?
Offline
#8 04. 06. 2023 20:10
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ Vojtěch Šebek:
Já nevím jestli vám to vyučující uzná, ten můj postup naráží na to, že pojem "začít nějakým prvkem" není podle mě moc dobře definován, resp. pokud to není upřesněno, tak lze začít podle mě libovolným prvkem....
"Máte úhel beta." "No to nemám."
Offline
#9 05. 06. 2023 09:59 — Editoval surovec (05. 06. 2023 09:59)
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ Vojtěch Šebek:
Podle mě jsou obě výše uvedené konstrukce chybné. BakyX zaměnil těžnice (řešil pro t_a), OiBobik zase chybně předpokládal, že |AT| = |AT'|, což samozřejmě není (ale možná jsem to jen blbě pochopil).
Začal bych konstrukcí jedné z těžnic, třeba tb. Následně oblouk k, kde může ležet A. Pak množinu bodů, kde může ležet pata těžnice Tc – to je oblouk k' s polovičním poloměrem než k, přičemž k a k' mají vnitřní dotyk v B. Pak už je to triviální, najdu těžiště T, kružnici (T; r = tc/3), z toho pak Tc, následně C a nakonec A.
Konstrukce začínající úhlem alpha asi jedině tak, jak píše check_drummer.
Co se týče podmínek, je to dost složité, kdysi jsem to dělal přes soustavu rovnic, jen sem připojím výsledek.
Podmínky
Offline
#10 05. 06. 2023 14:45
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
surovec napsal(a):
↑ Vojtěch Šebek:
Pak množinu bodů, kde může ležet pata těžnice Tc – to je oblouk k' s polovičním poloměrem než k, přičemž k a k' mají vnitřní dotyk v B.
Ahoj, tady jsem nepochopil jak ten oblouk k' kosntruovat, proč má poloviční poloměr než k a proč mají vnitřní dotyk v B.
"Máte úhel beta." "No to nemám."
Offline
#11 05. 06. 2023 14:54
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
Odchýlím se od svých zásad, kdy dávám rady postupně a napíšu sem celý postup, protože se mi to zdá poněkud komplikované. Možná bude ten postup blbě, tak i to bude z didaktického poheldu účelné - najít chybu. :-) Poctivý žák si může body 1)-6) zakrýt a postupně je odkrývat - jako postupné rady.
1) sestroj těžnici tb (označme ji BP)
2) sestroj těžistě T
3) sestroj kružnici k, ze které je vidět těžnice tb pod úhlem alfa - na ní někde bude ležet bod A
4) sestroj kružnici f se středem v T a poloměrem 2/3tc - na ní někde bude ležet bod C
5) Víme že bod C je obrazem bodu A ve středové souměrnosti se středem P, takže zobrazím kružnici k v této středové souměrnosti na kružnici k2 a k2 průnik f je hledaný bod C.
6) Bod A už sestrojíme snadno (aspoň někde nedám úplné řešení :-))
"Máte úhel beta." "No to nemám."
Offline
#12 05. 06. 2023 15:05 — Editoval surovec (05. 06. 2023 15:07)
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ check_drummer:
Na "konci" oblouku k přece leží bod B (na druhém konci je Tb). Někde na oblouku k leží také bod A. Pata těžnice na c (označme Tc) leží přesně mezi nimi (střed AB). Množinou těchto středů je pak opět kruhový oblouk, který má poloviční poloměr (páč 2|BTc| = |BA|) a společným bodem je bod B. Z obrázku to možná bude jasnější (představ si, jak se bod A posouvá po kružnici a jakou stopu zanechává bod Tc; je to stejnolehlost, kde se A zobrazuje do Tc, středem je B a koeficientem 1/2):
Odkaz
Offline
#13 05. 06. 2023 15:28
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ surovec:
Už je mi to jasné, to by taky šlo. tak jsem zvědav, jaký postup si tazatel vybere. :-)
"Máte úhel beta." "No to nemám."
Offline
#14 05. 06. 2023 16:49 — Editoval Honzc (05. 06. 2023 16:57)
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ Vojtěch Šebek:
Konstrukce viz. Obrázek (konstrukce stejná jako↑ check_drummer: pouze se začíná úhlem alfa, v obrázku červeně, doufám, že postup je z obrázku zřejmý)
Offline
#16 05. 06. 2023 17:15 — Editoval Honzc (05. 06. 2023 17:18)
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
↑ surovec:
1.úhel alfa (červený) (bod S)
2.rovnoběžka s "pravým" ramenem úhlu ve vzdálenosti tb/2
3.průsečík této rovnoběžky s "levým" ramenem je bod B
4. kolmice z bodu B na to "pravé rameno
5.bod P leží na té kolmici ve vzdálenosti /BP/=tb
6.kr.oblouk SPB (na něm bude ležet bod A)
7.kr.oblouk jako obraz kr.oblouku z 6. ve středové souměrnosti podle bodu P
8.těžište (bod T)
9.kružnice (T, 2tc/3)
10.bod C je průsečíkem kr.oblouku z 7. a kružnice z 9.
11. bod A je průsečíkem přímky CP a kr.oblouku z 6.
Tady 2 řešení
Offline
#17 05. 06. 2023 17:46
- Vojtěch Šebek

- Zelenáč
- Příspěvky: 6
- Škola: SPŠE Plzeň
- Pozice: Student, obor IT
- Reputace: 0
Re: Konstrukce trojúhelníku (alfa, t_b, t_c)
Děkuji Vám všem za veškeré poskytnuté rady, vyzkouším všechny zmíněné konstrukce a uvidím, ze které mi to půjde sestrojit nejlépe.
Offline
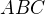 jestliže známe úhel
jestliže známe úhel  .
.