Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 20. 05. 2011 16:17 — Editoval Cheop (30. 05. 2011 08:49)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: rovnice elipsy
↑ Prokop:
Rovnice elipsy bude mít tvar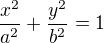
Pro elipsu platí: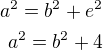
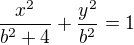
Přímka bude mít s elipsou 1 bod - je to tečna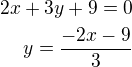 - dosadíme do elipsy
- dosadíme do elipsy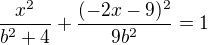 - úpravou:
- úpravou: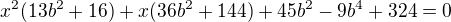 protože je to tečna řešíme tuto kvadratickou rovnici s parametrem b tak, aby diskriminant D = 0
protože je to tečna řešíme tuto kvadratickou rovnici s parametrem b tak, aby diskriminant D = 0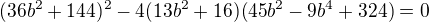
stroj odpověděl Odkaz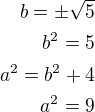
Rovnice elipsy: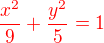

Nikdo není dokonalý
Offline