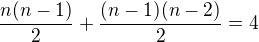Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 06. 2011 07:39
Kombinatorika
Množina všech přirozených čísel, pro která platí:
( n ) (n-1)
( 2 )+ ( 2 ) = 4
je podmnožinou intervalu:
a) <0,2)
b) <2,4)
c) <4,6)
d) <6,8)
e) žádná z možností
Nevím, jak upravit levou stranu. Předpokládám, že po úpravě se bude řešit kvadratická rovnice a to by už problém být neměl.
Offline
- (téma jako vyřešené označil(a) Dana1)
#4 06. 06. 2011 10:23 — Editoval Dana1 (06. 06. 2011 11:04)
- Dana1
- Host
Re: Kombinatorika
↑ firo:
Zdravím. Existuje ešte jedna možnosť riešenia - nazrieť do Pascalovho trojuholníka, podľa ktorého hneď vidno, že 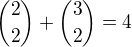
Z toho