Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 15. 06. 2011 17:18
Re: Goniometrické funkce
↑ tesarin:
sečíst  podle vzorce
podle vzorce 
a pak vytknout 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 15. 06. 2011 17:22 — Editoval Annnnnd (15. 06. 2011 19:01)
Re: Goniometrické funkce
↑ zdenek1:vyslo ti reseni jako 0 +2k pi; a (pi/2) + 2kpi ?
edit: jo je to blbe, sekl sem se ...
Offline
#4 15. 06. 2011 17:26
Offline
#5 15. 06. 2011 17:28 — Editoval tesarin (15. 06. 2011 17:29)
Re: Goniometrické funkce
↑ zdenek1:
Nějak mi to nejde... použil jsem ty vzorce, nevím jeslti dobře.. nevím jak dál :/
Offline
#6 15. 06. 2011 17:33
Re: Goniometrické funkce
↑ tesarin:
Tak si ještě jednou přečti CO máš sečíst. Sčítáš něco jiného, než ti radím.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 15. 06. 2011 17:38
Re: Goniometrické funkce
↑ zdenek1:a neslo by to resit jako sinx + 2sinx . cosx + sin (2x + x ) = 0 .a pak podle vztahu goniometrickych to upravovat a dosazovat..? ten tvuj postup bude asi rychlejsi ale zajima me jestli to nejde i takhle
Offline
#8 15. 06. 2011 17:42
Re: Goniometrické funkce
↑ zdenek1:
Moje chyba tak tedy..
.. ale stejně nevím jak dál, mohl bych poprosit?
Offline
#9 15. 06. 2011 17:45
Offline
#13 15. 06. 2011 18:03
Offline
#14 15. 06. 2011 18:04
Offline
#15 15. 06. 2011 18:07
#16 15. 06. 2011 18:10
Re: Goniometrické funkce
↑ tesarin:
Ano.
Nyní: kdy je součin dvou čísel nula?
A ještě drobnost. funkce kosinus je sudá, takže 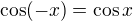
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#17 15. 06. 2011 18:18
Re: Goniometrické funkce
↑ zdenek1:
Díky za drobnost! ..
No když je jedno z těch čísel rovno 0? :D
Offline
#18 15. 06. 2011 18:25
Offline
#19 15. 06. 2011 18:32
#20 15. 06. 2011 18:34
Re: Goniometrické funkce
↑ tesarin:
Výsledky jsou v příspěvku #4
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#21 15. 06. 2011 18:40
Re: Goniometrické funkce
↑ zdenek1:
Nedaří se mi vyřešit druhou část čili 
... zkoušel jsem dál, ale nevím zda je to dobře...


.. to je zřejmě špatně, nevím :/
Offline
#22 15. 06. 2011 18:40
Re: Goniometrické funkce
↑ zdenek1:
sin2x(1+cosx) + sinx (2cos ^2 x )
2sinxcox(1+cosx) + sinx (2 . cos ^2 x)
2sinxcosx + 2sinx cox ^2 x + 2sinx cos ^ 2 x / : cosx
2sinx + 2sinxcosx + 2sinxcosx /: sinx
2 + 4 cosx = 0 ...
Offline
#25 15. 06. 2011 18:56
Re: Goniometrické funkce
↑ Dana1:to nemyslim.. jde o to ze zalezi jak tuto rci upravuji... pokud bych to resil jako sin2x(1 + cosx) + sinx (2 cosx cosx )
vyjde 2 + 4 cosx = 0 nebo 1 + cosx = 0 .. to jo ale pokud bych to resil jako zdenek1 tak tam vyjde to sin2x ( 1 + 2cosx) = 0..cili beru v uvahu sin2x = 0 a zaroven 1 +cos2x = 0 ....
Offline




 ?
? čili
čili 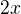





 nebo
nebo 