Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Analytická geometrie (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 06. 2011 09:19 — Editoval Miki314 (17. 06. 2011 09:27)
Analytická geometrie
Ahoj, potřebuju poradit se 2 příkladama..
1. - Máme zadány 2 přímky, jedna určená bodem M a vektorem a, druhá určená bodem B a vektorem b.
M = (1,2,3); vektor a = (1,1,1), bod B = (1,1,111), vektor b = (0,1,1);
Určete přímky p, které -
a) p se protíná s přímkou a pod úhlem 90 stupňů v bode M = (1,2,3)
b) p svírá s přímkou b úhel 60 stupňů.
Řešení - postupoval jsem tak, že když se p protíná s a pod úhlem 90 stupňů, tak si udělám rovnici, kdy cos 90 = v čitateli absolutní hodnota p1 + p2 + p3, jmenovatel odmocnina ze 3 * odmocnina z p1 na druhou + p2 na druhou + p3 na druhou. A druhá rovnice 1/2 = v čitateli absol. hodnota p2 + p3, jmenovatel odmocnina ze 2 * odmocnina z p1 na druhou + p2 na druhou + p3 na druhou. Vyřešil jsem tyto 2 soustavy a dosadil do 3. soustavy, která zněla odmocnina ze 2 * = odmocnina z p1 na druhou + p2 na druhou + p3 na druhou. Vyřešil jsem a dostal jsem hodnoty směrového vektoru přímky p. No a jelikož se p protíná s a v bodě M, tak M je i bod přímky p i a, takže přímka p je určená bodem M a vektorem p1, p2, p3. Je tento postup správný??
A druhý přiklad - Máme dánu kuželosečku obecnou rovnicí 4xy - y^2 - 2x - 1 = 0. Určete odchylku asymptot, v němž leží bod M = (2,0).
Řešení - vypočítal jsem si velký a malý diskriminant, z něhož vím, že se jedná o hyperbolu, no a dál absolutně netuším..
Děkuji za případné rady.. Tomáš
Offline
- (téma jako vyřešené označil(a) Miki314)
#2 17. 06. 2011 15:14 — Editoval Rumburak (17. 06. 2011 16:54)
Re: Analytická geometrie
Ad 1.
Tvůj popis postupu mi nepřitadá příliš srozumitelný, mnoho se v něm píše (a ne vždy přesně) o rovnicích a jednotlivých výrazech,
ale není mi z toho jasná matematická idea takového postupu.
Zřejmě je výhodné hledat přímku v parametickém tvaru. Víme o ní, že prochází daným bodem M , takže už jen zbývá
určit její směrový vektor  a parametrickou rovnici pak již snadno sestavíme.
a parametrickou rovnici pak již snadno sestavíme.
Dle zadání úlohy by o vektoru 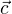 mělo platit:
mělo platit:
(I) je kolmý k vektoru  , což znamená, že
, což znamená, že 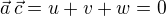 ,
,
(II) svírá 60 st. s vektorem  , což znamená, že
, což znamená, že
 ,
,
i toto rozepíšeme pomocí souřadnic . Obdržíme tak soustavu dvou rovnic o třech neznámých.
Připojíme ještě podmínku 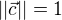 , tím se rovnice plynoucí z (II) zjednoduší a řešení pak vyjde téměř jednoznačně (až na koeficient (-1)).
, tím se rovnice plynoucí z (II) zjednoduší a řešení pak vyjde téměř jednoznačně (až na koeficient (-1)).
Ad. 2 . Urči asymptoty.
EDIT 3 . K nalezení aymptot hyperboly můžeme použít následující větu:
Přímka o parametrických rovnicích x = x(t) , y = y(t) je asymptotou hyperboly o rovnici H(x,y) = 0, právě když rovnice
H(x(t),y(t)) = 0 s neznámou t nemá řešení reálné ani imaginární (tj. alg. úpravou z ní odvodíme spor - např. tvaru 1 = 0).
Příště si ke každé úloze založ zvláštní téma.
Offline
#3 17. 06. 2011 18:08
Re: Analytická geometrie
↑ Rumburak:
Já právě tmu nerozumím, jak určit ty asymptoty... Protože když mám teda tu rovnici, tak z ní určím velký a malý diskriminant a tím jsem skončil, nevím jak dál určit ty asymptoty...
Offline
#4 20. 06. 2011 10:38 — Editoval Rumburak (20. 06. 2011 11:32)
Re: Analytická geometrie
↑ Miki314:
Tak k těm asymptotám:
Aspoň jedna z nich bude různoběžná s osou y , takže bude možno popsat ji rovnicí ve směrnicovém tvaru .
(0)  .
.
Na (0) lze pohlížet jako na parametrické vyjádření 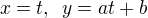 , tudíž nic nám nebrání použít větu uvedenou v ↑ Rumburak: .
, tudíž nic nám nebrání použít větu uvedenou v ↑ Rumburak: .
Zkoumáme tedy rovnici
(1) 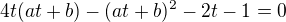 ,
,
s neznámou t , z níž úpravami postupně obdržíme
 ,
,
 ,
,
(2)  .
.
Aby byla splněna podmínka věty, nesmí mít rovnice (1) a tedy ani (2) žádné řešení, a to ani imaginární. Takže: na levé straně v (2) musí být
(v proměnné t) polynom stupně 0, tedy musí být splněna soustava rovnic 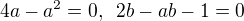 . Ta má dvě řešení:
. Ta má dvě řešení:
I. 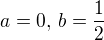 resp. II.
resp. II. 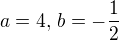 .
.
Jestliže libovolné z nich dosadíme do (2), dostaneme  , resp.
, resp.  ,
,
což v obou případech dá 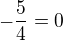 , tedy spor, takže taková rovnice (2) a tedy ani (1) pak nebude řešitelná, a to ani v komplezním oboru.
, tedy spor, takže taková rovnice (2) a tedy ani (1) pak nebude řešitelná, a to ani v komplezním oboru.
Přmky o rovnicích 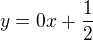 ,
, 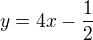 jsou tedy asymptotami dané hyperbpöly.
jsou tedy asymptotami dané hyperbpöly.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Analytická geometrie (TOTO TÉMA JE VYŘEŠENÉ)