Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzdálenost bodu od roviny (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 06. 2011 11:20
Vzdálenost bodu od roviny
Ahoj, potřebuju poradit s tímto příkladem: Určete vzdálenost bodu B = (-9,2,1,-5) od roviny Alfa:
x1 = 1-r
x2 = 2 + r - 2s
x3 = r + s
x4 = 3r - s
Absolutně netuším, co s tím. Napadlo mě převést parametrické vyjádření na obecnou rovnici roviny, ale to nevím jak. Každopádně vím, že musím najít kolmý průmět bodu B do Alfa... Ale jak, to netuším, když je rovina zadána parametricky... :)
Offline
- (téma jako vyřešené označil(a) Miki314)
#2 25. 06. 2011 14:02 — Editoval teolog (25. 06. 2011 14:02)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Vzdálenost bodu od roviny
↑ Miki314:
V tomto případě nelze obecnou rovnici roviny použít, protože v E4 neexistuje. Musíte pracovat s parametrickými rovnicemi.
Pomůže taková nápověda?
Obecně se snažíme spočíst vzdálenost bodu B od jeho kolmého průmětu Bp do podprostoru. Bod Bp určujeme jako ten bod podprostoru (popsaný pomocí parametrů), pro který je vektor B - Bp kolmý na generátory zaměření daného podprostoru (tím dostáváme potřebný počet rovnic pro neznámé parametry.
Offline
#4 25. 06. 2011 14:37 — Editoval teolog (25. 06. 2011 14:38)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Vzdálenost bodu od roviny
↑ Miki314:
Přesně tak. Takže mějme nějaký neznámý bod X, který leží v dané rovině, tedy souřadnice tohoto bodu můžu vyjádřit takto:![kopírovat do textarea $X=[1-r,2+r-2s,r+s,3r-s]$](/mathtex/be/bea5f3fe22e9ce05ccef5732f7f231a7.gif) . A teď sestavme vektor XB (kde bod B je tan zadaný), tedy
. A teď sestavme vektor XB (kde bod B je tan zadaný), tedy 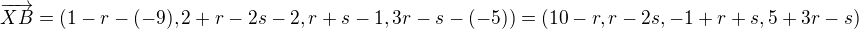 .
.
A nyní chceme, aby tento vektor byl kolmý na naší rovinu, tedy musí být kolmý na oba směrové vektory dané roviny. Takže musí platit:  a
a 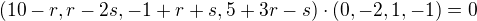 . Z tohoto spočítete hodnoty r a s a najdete hledaný průmět bodu B do roviny.
. Z tohoto spočítete hodnoty r a s a najdete hledaný průmět bodu B do roviny.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzdálenost bodu od roviny (TOTO TÉMA JE VYŘEŠENÉ)