Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Pomoc při důkazu matematickou indukcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 09. 2011 23:38 — Editoval apelttom (17. 09. 2011 23:47)
Pomoc při důkazu matematickou indukcí
Dobrý den,
učím se ze skript od pana docenta Jiřího Velebila a narazil jsem na příklad důkazu za pomoci matematické indukce. Pro uvedení do problému příklad podrobně rozepisuji, jak je ve skriptech (snad to není porušení nějakých práv...)
Dokažte, že nerovnost  platí pro všechna přirozená čísla
platí pro všechna přirozená čísla 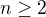
Tento příklad je zde popsán i s řešením a v indukčním kroku a použitím indukčního předpokladu se dostaneme k:
Poté následuje věta: Nyní by k ukončení důkazu indukčního kroku stačilo ukázat, že platí nerovnost 
A tuhle část právě nechápu. Proč musím ukázat, že je obsah závorek nezáporný? Vždyť i kdyby byl záporný, tak princip toho, že levá strana bude větší pořád platí.
Ocením jakékoliv nápady a názory a v případě potřeby tady rozepíšu i celý důkaz.
Děkuji a doufám, že jsem neporušil tak tucet pravidel o zakládání nových témat, jsem tu nový :-)
Offline
- (téma jako vyřešené označil(a) apelttom)
#2 18. 09. 2011 01:26 — Editoval OiBobik (18. 09. 2011 01:49)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Pomoc při důkazu matematickou indukcí
↑ apelttom:
Zdravím,
v indukčním kroku jde o to dokázat, že dokazované tvrzení platí pro n+1, tedy konkrétně nerovnost 
Levá strana nerovnosti je shodná s levou stranou tvojí nerovnosti. Pokud nyní dokážeme, že pravá strana tvojí nerovnosti je větší nebo rovna 1/2, z tranzitivity uspořádání již poplyne nerovnost výše. Proto je potřeba, aby výraz v závorce byl nezáporný.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 18. 09. 2011 15:41
Re: Pomoc při důkazu matematickou indukcí
↑ OiBobik:
Děkuji za pěknou a smysluplnou odpověď, teď mi to došlo. Uzavírám téma jako vyřešené.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Pomoc při důkazu matematickou indukcí (TOTO TÉMA JE VYŘEŠENÉ)