Matematické Fórum

Sulfan · 08. 10. 2011 20:17

Ahoj,

počítám jeden příklad, u kterého jsi nejsem jistý zdůvodněním výsledku, proto bych chtěl požádat o radu, popřípadě kontrolu správnosti postupu.

Má se zjistit, že daná podmnožina vektorového prostoru polynomů složená z vektorů 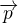$\overrightarrow{p}$ tvoří vektorový prostor V nad $\mathbb{C}$ , pro které platí, že
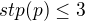$stp(p) \leq 3$ , neboli, že stupeň x je roven nejvýše 3.

Ve výsledcích je napsáno, že o vektorový prostor nad C nejde.

Můj postup je následující:

Typické vektory takového prostoru budou ve tvaru: 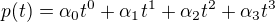$p(t)=\alpha _{0}t^{0}+\alpha _{1}t^{1}+\alpha _{2}t^{2}+\alpha _{3}t^{3}$

a pro takové vektory a operace definované bodově platí všechny axiomy vektorového prostoru, s výjimkou nulového polynomu (nulového vektoru), který nemá svůj stupeň definován, a tak by do V nemusel patřit. Nejsem si však jistý, jestli tu vlastnost, že nejde o vektorový prostor zkazí pouze existence nulového vektoru nebo i něco dalšího.

Děkuji za odpověď.

anes · 08. 10. 2011 21:56

A nemají tam nějak nestandardně zavedené operace, že by byl třeba problém s uzavřeností (pokud už jsi ty axiomy ověřil správně)? Splnění všech axiomů je samozřejmě potřeba a je možné, že si na příkladu máte uvědomit, že je tam potřeba ten nulový polynom extra přihodit. Bylo by to dost hnidopišské (většinou se zahrnutí nulového prvku bere jako samozřejmost, někdo si i definuje st. 0 pol. jako -1, aby tohle nemusel řešit), ale možné to je.

Sulfan · 08. 10. 2011 22:41 — Editoval Sulfan (08. 10. 2011 22:43)

↑ anes: Operace jsou v prostoru polynomů $P$ definovány standardně (bodově), tudíž:

$\left (\forall p\in P \right )\left (\forall q\in P \right )\left (\forall t\in \mathbb{C} \right )((p\oplus q )(t)=p(t)+q(t))$

$(\forall \alpha \in \mathbb{C}) (\forall p\in P ) (\forall t\in \mathbb{C} )((\alpha \otimes p )(t)= \alpha \cdot p(t))$

OiBobik

↑ Sulfan:

Tam by neměl být žádný problém, pokud je definován stupeň polynomu p(x)=0 (někdy se, myslím, definuje). Jediná další věc, co mě napadá, je, že myslí polynomy s reálnými koeficienty (což by bylo teda taky dost hloupé zadání příkladu : )) ) - pak by to skutečně vektorový prostor nad C nebyl,jelikož to není uzavřené na násobení skalárem (to mě napadá jen proto, že to těleso C je nějak podezřele specifické).

LukasM · 09. 10. 2011 04:55

↑ Sulfan:
Ahoj. Pokud se nepletu, tak jsi z FJFI, a jde o příklad z Pytlíčkových skript.

Podle Pytlíčka není stupeň nulového polynomu definován, takže v té množině není nulový prvek, a tedy to nemůže být vektorový prostor. Nic dalšího v tom nevidím.

vanok · 09. 10. 2011 05:19 — Editoval vanok (09. 10. 2011 05:24)

ahoj ↑ Sulfan:

V http://sk.wikipedia.org/wiki/Mnoho%C4%8Dlen najdes <<. Nulový polynóm p(x) = 0 sa niekedy označuje ako polynóm stupňa −1.>>
Niektori autory uvedu konvenciu <<nulovy polynom la stupen $-\infty$ >>

A tak vdaka tomu nemas ziadny problem ...

Srdecne Vanok

Sulfan · 09. 10. 2011 09:18

Díky všem za odpověďi, zapomněl jsem napsat, že má polynom komplexní koeficienty, tudíž by se uzavřenost na operace neměla zkazit.

↑ LukasM: Jsem téhož názoru. :)

↑ vanok: Ano, záleží na definici stp(0), ale protože jde o dohodu, tak se v tomto případné zdroje liší.

Vše je teď asi jasné, řešení tohoto zadání zřejmě závisí na konvenci.

vanok · 09. 10. 2011 11:33

↑ Sulfan:

Som rad ze ti to pomohlo.
Nezabudni sa spytat ucitela na jeho dohodu alebo konvenciu.

Srdecne Vanok

Matematické Fórum

#1 08. 10. 2011 20:17

Ověření vektorového prostoru

#2 08. 10. 2011 21:56

Re: Ověření vektorového prostoru

#3 08. 10. 2011 22:41 — Editoval Sulfan (08. 10. 2011 22:43)

Re: Ověření vektorového prostoru

#4 08. 10. 2011 23:44 — Editoval OiBobik (08. 10. 2011 23:45)

Re: Ověření vektorového prostoru

#5 09. 10. 2011 04:55

Re: Ověření vektorového prostoru

#6 09. 10. 2011 05:19 — Editoval vanok (09. 10. 2011 05:24)

Re: Ověření vektorového prostoru

#7 09. 10. 2011 09:18

Re: Ověření vektorového prostoru

#8 09. 10. 2011 11:33

Re: Ověření vektorového prostoru

Zápatí