Matematické Fórum

ninja · 22. 06. 2008 22:20

Zdravim, potreboval bych poradit s priklady.

$f_n(x)=e^{n(x-x^2)}$

obor konvergence, stejnosmerne konvergence a lokalni stejnosmerne konvergence.

nevim na co pekneho si prevest to e

${\lim}\limits_{a \to \infty} \sum_{n=1}^{\infty} x/{(n(1+nx^2))}$

Vyjde 0 ,ale jaka veta mi dovoluje prepsat na $\sum_{n=1}^{\infty} {\lim}\limits_{a \to \infty} x/{(n(1+nx^2))}$

Mocnina rada $\sum_{n=1}^{ \infty} (x-1)^n /{(n2^n)}$

Obor konvergence celkem jednoduchej, ale jak spocitam soucet v oboru konvergence.

Diky za rady a za pomoc, na konci zk uz mi to moc nemysli

Marian · 23. 06. 2008 23:15

↑ ninja:

U druheho prikladu lze postupovat velice snadno. Pokud to spravne chapu, ma tam vsude byt limita pro $x\to +\infty$ . Lze tedy bez ujmy na obecnosti predpokladat, ze cislo x je jiz kladne, tzn. predpokladam, ze x>0. Plati dale snadny odhad pro nami uvazovane hodnoty realnych cisel x

$\frac{x}{n(1+x^2n)}=\frac{\frac{1}{x}}{n\left (\frac{1}{x^2}+n\right )}\le\frac{\frac{1}{x}}{n^2}.$

Odtud je

$0\le\sum_{n=1}^{\infty}\frac{x}{n(1+x^2n)}=\sum_{n=1}^{\infty}\frac{\frac{1}{x}}{n\left (\frac{1}{x^2}+n\right )}\le\sum_{n=1}^{\infty}\frac{\frac{1}{x}}{n^2}.$

Protoze ale uvazujeme kladna cisla x a rada $\sum_{n=1}^{\infty}\frac{1}{n^2}$ konverguje (absolutne), plati odhad

$0\le\sum_{n=1}^{\infty}\frac{x}{n(1+x^2n)}\le\frac{1}{x}\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{1}{x}\cdot\frac{\pi ^2}{6}.$

Tady je uz lhce videt, ze limitni prechod pro 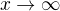$x\to \infty$ implikuje

$0\le\lim_{x\to\infty}\sum_{n=1}^{\infty}\frac{x}{n(1+x^2n)}\le\lim_{x\to\infty}\frac{1}{x}\cdot\frac{\pi ^2}{6}=0\cdot\frac{\pi ^2}{6}=0.$

Proto

$\lim_{x\to\infty}\sum_{n=1}^{\infty}\frac{x}{n(1+x^2n)}=0.$

Marian · 23. 06. 2008 23:23

Treti priklad take neni tezky. Tady staci naspat

$\sum_{n=1}^{\infty}\frac{(x-1)^n}{n2^n}=\sum_{n=1}^{\infty}\frac{\left (\frac{x-1}{2}\right )^n}{n}.$

Uvazime-li, ze $\sum_{n=1}^{\infty}\frac{q^n}{n}=-\ln (1-q)$ pro |q|<1 a take pro q=-1, mas snadno soucet tve rady, polozis-li q=(x-1)/2.

Spise tedy bude pro tebe zajimave, jak nalezt soucet rady $\sum_{n=1}^{\infty}\frac{q^n}{n}$ . Tady si budes muset rochu pohrat se stejnomernou konvergenci geometricke rady $\sum_{n=1}^{\infty}q^{n-1}$ . Jeji soucet znas, polomer stejnomerne konvergence (vzhledem k q) je jasny - je to mocninna rada. Uvaz, za jakych podminek je mozno integrovat tuto radu clen po clenu a dokaz tak formulku vyse s prirozenym logaritmem.

Marian · 23. 06. 2008 23:35 — Editoval Marian (23. 06. 2008 23:48)

U prvniho prikladu zkusim napovedet.

Rozdel si realnou primku s hodnotami promenne x pomoci nulovych bodu kvadraticke funkce $g(x):=x-x^2=x(1-x)$ . Najdes dva nulove body (x_1=0 a x_2=1). Funkce g(x) bude zaporna na intervalech (-oo,0) a (1,+oo). Naopak, na intervalu (0,1) bude funkce g(x) nabyvat kladnych hodnot, nicmene bude platit g(x) je mensi nebo rovno 1/4 (najdi si y-ovou souradnici vrcholu paraboly g(x)).

Limitni funkce k funkci f_n(x) bude f(x)=0 pro vsechna x z interval (-oo,0) a (1,+oo). Pro x=0 a x=1 bude f(x)=1 a pro zbytek hodnot ciselne primky dostanes, ze limitni funkce je f(x)=+oo, coz jiste neni realna funkce (s kolegou nazyvame tento pripad neco jako "Diracova daň").

Ted uz znas, jak vypada limitni funkce, takze s ostatnimi vecmi bys mohl hnout treba sam.

Pozn.: ak si predstavit "e"? "e" je tzv. Eulerovo cislo (= zaklad prirozeneho logaritmu ln(x)). Plati snadno overitelny odhad (z definice tohoto cisla - viz mnoho zdroju informaci na webu) 2<e<3. To bude stacit k dokonceni tech vypoctu vyse.

Matematické Fórum

#1 22. 06. 2008 22:20

konvergence rad - priklady

#2 23. 06. 2008 23:15

Re: konvergence rad - priklady

#3 23. 06. 2008 23:23

Re: konvergence rad - priklady

#4 23. 06. 2008 23:35 — Editoval Marian (23. 06. 2008 23:48)

Re: konvergence rad - priklady

Zápatí