Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Trojný integrál OBLASTI VÁLCE (TOTO TÉMA JE VYŘEŠENÉ)
#2 02. 11. 2011 23:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál OBLASTI VÁLCE
Zdravím,
podle rovnice x^2+y^2=z^2 bych našla kvadratickou plochu - (1), podmínky z<1 bych vymezila rovinou v z=1 (oblast pod rovinou). Ten dolní trychtýř pod z=0 by nebyl omezen, nechybí ještě nějaká podmínka v zadání? Děkuji.
Offline
#4 04. 11. 2011 00:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál OBLASTI VÁLCE
↑ marcel58:
děkuji, měla bych stejně - za předpokladu, že kužel je jen jeden (nad rovinou xOy). Ve všech nerovnicích předpokládám znaménko 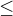 (< máš asi jen z úsporných důvodů).
(< máš asi jen z úsporných důvodů).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Trojný integrál OBLASTI VÁLCE (TOTO TÉMA JE VYŘEŠENÉ)