Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 22. 07. 2008 22:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
Zdravím :-)
V těchto příkladech se bude nejvíc používat vtip o matematikovi, co vaří čaj - nejdřív "vylit konvici"
Používáme něco, jako substituci, ale nemusíme to nějak podrobně rozepisovat:
Je to vidět?
Offline
#27 22. 07. 2008 23:18 — Editoval jelena (28. 07. 2008 22:40)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
Pokračování:
je to postup ve zkrácené podobě - pouze základní úpravy, korektní použití úprav není samozřejmé a je dokazováno v materiálech mat. analýzy.
dělení mnohočlenu mnohočlenem: 
Z předchozího příkladu vím, že do mocniny musím dostat obracený druhý sčítanec, tak ho tam pošlu a upravím - doplním, tak výraz v mocnině zůstal beze změny: 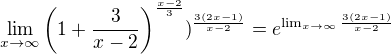
V podstatě hledáme tuto limitu: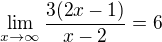
OK?
Editace: korektní důkaz, že tato úprava mohla být použita, je uveden u kolegy BrozekP v příspěvku 44 (souhlasím s jeho námitkou a doporučují další debatu v tomto tématu. Děkuji kolegovi za důsledný přístup :-)
Offline
#28 22. 07. 2008 23:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity

Zde se musí jen dát pozor na to, že x se bliží 0 zleva - pokud si predstaviš funkci y=1/x v III. kvadrantu, tak to bude jasné (x se bliží 0, funkce "odchází" do -oo). Máme "hocičo" na "-oo" a to je 1/"hocičo na +oo" . OK?
Offline
#31 23. 07. 2008 15:03 — Editoval matoxy (23. 07. 2008 15:46)
Re: Limity
Pekný deň, (aj keď trochu upršaný)
Príklad 86, je jasný, nejak ma zmiatlo to - pred nekonečnom.
Ale zvyšné dva akosi nie. V tomto príklade  chápem, ako sme zaviedli to k a k^-1 do mocniteľov, aj v zlomku ako sme to preveidli. Keďže píšete, že používate vz?ah:
chápem, ako sme zaviedli to k a k^-1 do mocniteľov, aj v zlomku ako sme to preveidli. Keďže píšete, že používate vz?ah: 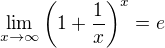 , tak myslím, že v tejto limite:
, tak myslím, že v tejto limite:  sa nejako dajú vykráti? tie k^-1, 49m bz sme dostali
sa nejako dajú vykráti? tie k^-1, 49m bz sme dostali  a to oni ponúkajú ako výsledok. Ale nechápem ako sa tie k-áška krátia. Bolo by možné vysvetli? prosím?
a to oni ponúkajú ako výsledok. Ale nechápem ako sa tie k-áška krátia. Bolo by možné vysvetli? prosím?
Príklad 63. mám ten istý problém. Ostatné z neho rozumiem.
EDITACE: + ešte by som chcel vedie?, či je správne nasledujúce riešenie: príklad 53. 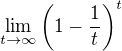 Zavedieme substitúciu q=-t a píšeme:
Zavedieme substitúciu q=-t a píšeme: 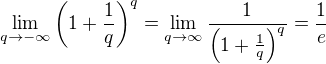 . Ide mi hlavne o to, či som mohol meni? tie znamienka pri nekonečne.
. Ide mi hlavne o to, či som mohol meni? tie znamienka pri nekonečne.
You know who
(or maybe not)
Offline
#32 23. 07. 2008 15:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
Zdravím :-) zde jsem vysvětlovala podrobně http://forum.matweb.cz/viewtopic.php?id=661
Nekrátíme, ale naopak rozšiřujeme k, aby mocnina a "jmenovatel" - bylo stejně. OK?
Offline
#33 24. 07. 2008 21:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
Ještě doplním k poslední otazce - "zda bylo možné měnít znaménka nekonečná".
Asi tak: obecně - pokud se použije substituce, návazně se musí změnit i jeji vlastnost ("kam se bliží").
V tomto konkretním případě bych byla trochu opatrnější - mám za to, že samotný důkaz pozoruhodné limity je postaven na směřování x k +oo. Změnou "směřování nové proměnné" bych asi porušila platnost vztahu. A proto veškeré úpravy provádíme tak, aby t -> +oo bylo zachováno.
výsledek je absolutně stejný, ale z mého pohledu více koréktní úprava.
To je můj pocit k použití substituce v tomto případě - snad sem koukne nekdo ze stranek VŠ, děkuji :-)
Offline
#34 26. 07. 2008 16:59 — Editoval matoxy (26. 07. 2008 17:01)
Re: Limity
Zdravím. Pár dni som sa neozval, lebo som bol odcestovaný, no už som tu a môžem počíta?:).
Najskôr by som mal otázku k tomu článku, na ktorý ste ma odkázali, je tam totiž takáto limita:
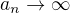
Má nejaký špeciálny význam, že je tam a_n a nie je ponechané n?
Príklad 63. je už jasný: 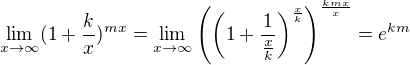 .
.
Príklad 65. mi vychádza troch inak ako je uvedené tam. 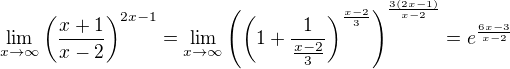 . Uvádzajú však výsledok e^x.
. Uvádzajú však výsledok e^x.
Príklad 53 pochopené:). Ďakujem.
You know who
(or maybe not)
Offline
#35 26. 07. 2008 17:14 — Editoval matoxy (26. 07. 2008 21:08)
Re: Limity
A ešte by som sa chcel spýta? na túto limitu: 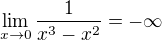 .
.
Stačí k tomuto príkladu také zdôvodnenie: Keďže platí: x^3 je, pre čísla menšie od 1 a väčšie od -1, menšie ako x^2 a menšie číslo mínus väčšie je záporné č. a zároveň platí, že ak x->0 tak x^-1=oo, tak potom je vyššie uvedená limita rovná -oo?
You know who
(or maybe not)
Offline
#37 26. 07. 2008 18:26
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
Offline
#39 26. 07. 2008 21:24 — Editoval BrozekP (26. 07. 2008 21:25)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
Offline
#40 26. 07. 2008 21:28 — Editoval matoxy (26. 07. 2008 21:32)
Re: Limity
A ešte by som potreboval pomôc? s týmto príkladom: (je to príklad č. 118)  . V Help je napísané, že treba použi? binomickú vetu. Čitateľ som skúsil rozloži? pomocou binomickej vety a vyňatím upravil na:
. V Help je napísané, že treba použi? binomickú vetu. Čitateľ som skúsil rozloži? pomocou binomickej vety a vyňatím upravil na:  , ale s menovateľom som si nevedel rady.
, ale s menovateľom som si nevedel rady.
EDITACE: BrozekP jasné:)
You know who
(or maybe not)
Offline
#41 26. 07. 2008 21:49 — Editoval BrozekP (26. 07. 2008 21:50)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
Podle mě je tady binomická věta zbytečná, stačí zlomek krátit 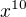 , jako když máš jednoduchý podíl polynomů, jenom to
, jako když máš jednoduchý podíl polynomů, jenom to 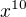 se dostane do těch závorek jako x. Limita by tedy měla vyjít 10.
se dostane do těch závorek jako x. Limita by tedy měla vyjít 10.
Offline
#42 27. 07. 2008 00:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ BrozekP:
Zdravím :-)
Začnu od konce (uvadim čísla zadaní, jak to ma kolega matoxy v odkazované strance www.mojeskola.cz ):
118. napověda směrem k binomické větě je pouze z toho důvodu, aby se uvědomila úprava, kterou navrhuješ - samozřejmě, není nutné rozepisovat všechno.
65. - moje úprava v příspěvku 27 není korektní?
105. - prispěvky 22, 23 - je to zvladnuto, ale nevím, jak v souladu s napovědou použit větu o trech limitách (dle mého to překračuje možnosti střední školy - nebo mi něco uniklo)?
moje vysvětlění v příspěvku 31 - 33 - je to myšleno správně? nebo to zbytečně komplikuji?
Moc děkuji za pomoc :-)
Offline
#44 27. 07. 2008 18:04 — Editoval BrozekP (28. 07. 2008 00:47)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
Také zdravím, to je ale věcí najednou :-) Takže postupně:
118: Mě to stále přijde nepodstatné, že se to dá rozepsat binomickou větou. I kdyby v těch závorkách byl třeba trojčlen, kde binomickou větu nepoužiješ, tak to x dovnitř stejně nacpeš (jak ukážu dál)
65: Já jsem to tvoje řešení přehlídl, z příspěvku ↑ matoxy: jsem to považoval za nevyřešené, tak jsem to vyřešil :-) Jinak ta tvoje úprava neni přímo podle žádné věty kterou znám. Za jistých okolností (včetně těchto) je tvoje úprava správná, ale podle mě by si zasloužila mnohem víc rozvinout:
Předpokládejme, že máme posloupnosti  a
a 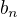 a že existují vlastní limity
a že existují vlastní limity  a
a 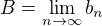 . Pak můžu psát
. Pak můžu psát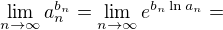
Podle věty o limitě složené funkce (ta ale nemůže být použita před úpravou, kterou jsem na předchozím řádku udělal)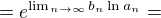
podle aritmetiky limit a spojitosti logaritmu v A je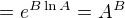
což je to, co jsi udělala. Jestli ta úprava jde zdůvodnit nějak lépe, tak budu rád, když mi ji vysvětlíš :-)
Budu pokračovat v dalším příspěvku, už je toho nějak moc :-)
Offline
#46 27. 07. 2008 19:34 — Editoval BrozekP (27. 07. 2008 19:35)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
↑ jelena:
"moje vysvětlění v příspěvku 31 - 33" - to mi trochu osvětlilo, co vlastně děláš - ty používáš tvrzení:
Pokud 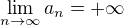 a
a 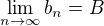 pak
pak  .
.
Toto tvrzení je naštěstí pravdivé :-) Podle mě tohle tvrzení ale neni triviální (ale lehce dokazatelné), takže takováhle tvrzení používat ano, ale být si jistý, že platí. Na základě čeho jsi tu úpravu prováděla? Věděla jsi, že to je správně, nebo to bylo spíš intuitivní?
Nemáš tam nic tak hrozného, napsal jsem jen, že to tim zavání, tim jsem chtěl naznačit, že možná používáš věty, které neexistují :-)
Jinak tvoje vysvětlení jak řešit tyhle příklady je opravdu polopatické :-), ale myslím, že správné.
↑ matoxy: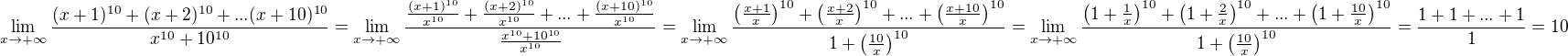
Bylo toho dost, tak pokud jsem něco nezodpověděl, tak mě upozorněte :-)
Offline
#47 27. 07. 2008 23:19 — Editoval jelena (28. 07. 2008 19:08)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ BrozekP:
To je tak:
- intuici určitě téměř nepoužívam, myslím, že ani vůbec nepoužívam (a to nejen v matematice :-).
Používám:
- dlouhodobě nacvičené postupy (chování "stonožka") - pak nabízím svoje nudné standardní návody (občas ale váhám, zda tento postup nemá nejaké omezení, které si zrovna neumím představit nebo dohledat - proto dotazy, co jsem tady měla).
- nápady a doporučení, které úplně dokonale nemám nacvičeno, ale kterým rozumím alespoň principialně a vím, že dokážu dotáhnout do konce za použití dostupné literatury.
- pokusy v oboru, o který se zajímám (statistika a pravděpodobnost) ke spravedlivé kritice od ostatních :-)
Tady je trochu jiný problém - základy mat. analýzy - jek se berou na střední škole, musí se potykat s určutým omezeným prostorem a proto hodně "pouček a pomůcek" se používá bez důkazu, jen jak nástroj. Něco je možné bez obav, že to zanechá negativní následek pro pozdější studium, na jiné je potřeba upozornit.
Kolegovi matoxy doporučím, a? rovnou začné číst V. Jarníka, kterého poskytl Marian (děkuji :-). Absolutně nemám obavy, že něco bude činit problém - je to zcela snadná četba.
Jelikož kolega matoxy má úplně jiný zájem, než běžný středoškolak (kterému by stačilo pár pouček a známka z pisemky), nechcí ponechávat bílá místa a prosím o pomoc někoho od "opravdových matematiků" :-)
K naši debatě o tom, co používám - řekla bych, že já tam vídím více limitu složené funkce, než dvě posloupnosti - můj návod úpravy je "polopatická transformace". :-)
Ještě k "binomické větě" - tvoje úprava je zcela jasná a přehledná, ale, uznej :-) - pokud to je potřeba napsat do "krátké nápovědy", tak tomu řekneme "binomická věta" - definuj svůj postup srozumitelně středoškolakovi a pošlí ho autorovi webu :-)
A ještě chybí "použití věty o trech limitách" v příkladu 105 (příspěvky 22, 23) - netrvám na tom, budu vděčna, když se to osvětlí :-)
Offline
#48 27. 07. 2008 23:44
Re: Limity
BrozekP ach áno, samozrejme. Ja som sa ten čitateľ pokúšal deli? pomocou nejakého vyňatia, alebo takého niečoho. Teraz to aj mne už vyšlo 10. Možno majú na stránke preklep, o jednu nulu viac.
Jelena: Toho V. Jarníka som si stiahol, len je to v takom čudnom formáte pdf.bz a neviem cez čo to otvori?. Neviete náhodou?
You know who
(or maybe not)
Offline
#49 28. 07. 2008 01:15
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
↑ jelena:
editováno, takže teď ještě tu nepěknou hrůzu musíš smazat z citace v příspěvku 45, a? jsou smazány všechny veřejné důkazy :-) Omlouvám se, že jsem tě nařkl z vytváření nepěkných hrůz. Přimlouval bych se ale za to, abys tyto netriviální kroky v budoucnu nějak komentovala, protože by to někoho mohlo vést k mylnému názoru, že může kdekoliv ve výrazu "zalimitit" a pokračovat dále v úpravách.
Pokud tam vidíš limitu složené funkce, tak co je vnější a co vnitřní funkce?
K binomické větě - při výpočtu limity jsem ji vůbec nepoužil, takže bych ji do nápovědy logicky nedával. Tenhle postup mi přijde naprosto přirozený i pro středoškoláka a jednodušší než s binomickou větou. Vždy? na střední se při počítání limit běžně používá úprava krácení zlomku nejvyšší mocninou x a běžně středoškoláci upravují výrazy s mocninami (tím myslím 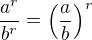 )
)
To použití věty o třech limitách - (vůbec nechápu, kam se to podělo, jsem si jistý, že jsem to do jedné z těch zpráv psal a teď to tu neni. Asi jsem si to nějak omylem smazal) nenašel jsem žádný jiný způsob než které jste uváděli, takže známé limity 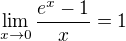 (uvádějí ji až v další lekci, to asi bude jejich chyba) a
(uvádějí ji až v další lekci, to asi bude jejich chyba) a 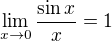 (jak sami ukazují v lekci 1, takhle limita se dá dokázat podle věty o třech limitách a tim si vysvětluji tu nápovědu).
(jak sami ukazují v lekci 1, takhle limita se dá dokázat podle věty o třech limitách a tim si vysvětluji tu nápovědu).
Offline
#50 28. 07. 2008 08:44
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
Řešili jste tady limitu 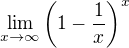 , že když se udělá substituce, tak nová proměnná jde do minus nekonečna. Úpravy, které dělá Matoxy v editaci příspěvku 31, podle mě nejsou dobře (i když dávají správný výsledek). Jelena má pravdu, že je tady potřeba být opatrnější, zase jsi provedla ten tvůj krok, který bych radši vysvětlil :-). Předpokládám, že nepovažuješ za důležité, jestli
, že když se udělá substituce, tak nová proměnná jde do minus nekonečna. Úpravy, které dělá Matoxy v editaci příspěvku 31, podle mě nejsou dobře (i když dávají správný výsledek). Jelena má pravdu, že je tady potřeba být opatrnější, zase jsi provedla ten tvůj krok, který bych radši vysvětlil :-). Předpokládám, že nepovažuješ za důležité, jestli  ve výrazu
ve výrazu 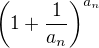 jde k plus nebo minus nekonečnu, abys použila ten tvůj postup. To je pravda a já to jen pro klid duše na zadaném příkladu ukážu (možná to jde jednodušeji, ale to nevim jak):
jde k plus nebo minus nekonečnu, abys použila ten tvůj postup. To je pravda a já to jen pro klid duše na zadaném příkladu ukážu (možná to jde jednodušeji, ale to nevim jak):
Takže mějme  záporné (třeba -1, jako v příspěvku 33, to už si dosaďte co chcete, o tu zápornost jde proto, aby ta jednoduchá substituce vedla ke směřování k minus nekonečnu)
záporné (třeba -1, jako v příspěvku 33, to už si dosaďte co chcete, o tu zápornost jde proto, aby ta jednoduchá substituce vedla ke směřování k minus nekonečnu)
teď provedu substituci  , takže
, takže 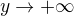
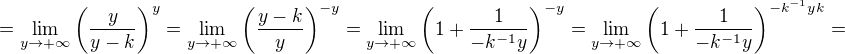
Nyní provedu substituci  , protože je ale k záporné, tak opět
, protože je ale k záporné, tak opět 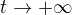
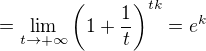
Offline

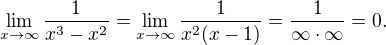
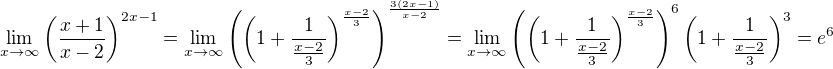
 na 6? Veď ak hore vyjímem 6-ku, tak mi ostane
na 6? Veď ak hore vyjímem 6-ku, tak mi ostane 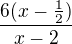 a z toho 6 nedostanem nie?
a z toho 6 nedostanem nie?