Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 08. 2008 11:29
Posloupnosti
Ahoj prosím o pomoc s tímto příkladem...
Posloupnost je dána rekurentně:
a1 = -1
an+1 = an + 2n + 1
a)napiště prvních pět členů
b)načrtněte graf posloup-
c) Rozhodněte, zda se jedná o posl. arit. nebo geom..
řešení: -1, 4, 11, 20, 31, 44
rostoucí posloupnost
není ani arit ani geom...
prosím o nějaké vysvětlení, nechápu jak k tomu došli a vůbec ten rekurentní zápis... Díík
Offline
#2 11. 08. 2008 12:11 — Editoval Cheop (11. 08. 2008 12:19)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Posloupnosti
Rekurentně znamená opakovaně tvořit členy posloupnosti podle určitého předpisu. Následující člen posloupnosti závisí na předcházejícím.Výpočet následujícího členu je dán určitým vztahem
Předpis je dán vztahem:









Nikdo není dokonalý
Offline
#3 11. 08. 2008 12:19
Re: Posloupnosti
Ahoj.
Rekurentní zadání znamená, že člen je závislý na členu předcházejícím.
Máš člen 
Pokud chceš člen  Tak podle zadání vezmeš hodnotu
Tak podle zadání vezmeš hodnotu  , k ní přičteš
, k ní přičteš 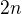 , kde n je index akutálního členu, tedy 2 a plus 1.
, kde n je index akutálního členu, tedy 2 a plus 1.
Celkem tedy 
Dále člen  . Zde je
. Zde je  a n=3
a n=3
Takže 
A tak dále.
Jestli je posloupnost rostoucí se pozná tak, že každý člen je větší než jeho předchozí člen, což jde zde splněno na první pohled.
Aby byla posloupnost aritmetická, musely by její členy narůstat o stejný kus. Protože ale z a1 na a2 je skok o 5 a z a2 na a3 už o 7, nemůže se jednat o arimtetickou poslopnost.
Aby byla geometrická, muselo by proi každý člen platit, že vznikne ze členu předchozího, vynásobením koeficientem q, ale ten musí být pro všechna n stejný. Tady to zřejmě neplatí. Už jenom proto, že od druhého členu jsou všechny kladné a první je záporný.
Graf nakreslíš jednoduše, to snad víš.
oo^0 = 1
Offline
#4 11. 08. 2008 14:20
Re: Posloupnosti
↑ Cheop:
Slovo rekurentní neznamená opakovaně tvořit členy posloupnosti podle určitého předpisu. Slovo rekurentní znamená opakující se ve smyslu vedoucí dozadu. Toto slovo se automaticky, popř. primárně nevztahuje na posloupnosti. Ale pravdou je, že v tomto příspěvku se jeví jako pravděpodobné, že toto slovo bereš v reakci na minulý příspěvek právě ve vazbě na posloupnosti. Na druhou stranu nelze souhlasit s tím, že rekurentně znamená (vztaženo na posloupnost), že její členy utvoříme (vypočteme - je-li to obecbě vůbec možné, nebo nějak zkostruujeme) opakovaně podle jistého předpisu. Museli bychom doplnit pomocí členů předcházejících. To červeně označené mi tam chybělo. Protože když konstruujeme nebo počítáme členy číselné posloupnosti, pak to provádíme taktéž opakovaně (tedy jeden za druhým).
To je ale jen formalita. Větší chybu pak vidím v tom, že píšeš  , ale proměnná n tam již nemá co dělat. Musí se důsledně nahrazovat všechny proměnné, ne jenom několik prvků. Tedy správně má být
, ale proměnná n tam již nemá co dělat. Musí se důsledně nahrazovat všechny proměnné, ne jenom několik prvků. Tedy správně má být  . V dalším řáku to je již správně, ale pak nechápu patrně správně smysl toho "mixovaného" meziřádku. Totéž se opakuje i v dalších řádcích tvého výpočtu.
. V dalším řáku to je již správně, ale pak nechápu patrně správně smysl toho "mixovaného" meziřádku. Totéž se opakuje i v dalších řádcích tvého výpočtu.
U ↑ ttopiho: je problematika vystižena lépe.
Nemám zájem nikoho shazovat a ani tak nečiním svým příspěvkem. Chtěl jsem jen poukázat na chyby, které se často dělají.
U samotného Karola pak v zadání také chybí několik věcí, ale nevím, zda-li to již takto neopsal z nějaké knihy.
Offline
#6 11. 08. 2008 15:00 — Editoval Marian (11. 08. 2008 15:47)
Re: Posloupnosti
↑ Cheop:
Přesně tak. Pokud je dána číselná posloupnost  , kde
, kde  a
a  , pak je tvůj výpočet korektní a Karolův chybný. Ale problém je také v tom, že v jeho zápisu může být chyba, protože mohl zapomenout na nějakou závorku. Navíc je jistě platný vztah
, pak je tvůj výpočet korektní a Karolův chybný. Ale problém je také v tom, že v jeho zápisu může být chyba, protože mohl zapomenout na nějakou závorku. Navíc je jistě platný vztah
a tedy rozdíly po sobě jdoucích členů budou v absolutní hodnotě (neřekl jsem totiž v jakém pořadí) tvořit aritmetickou posloupnost. Dá se také z toho říci, že posloupnost  daná rekurentně jako výše, je tedy aritmetickou posloupností druhého řádu. Těžko říci, co Karol studuje a jestli je na jeho SŠ obeznámen s pojmem aritmetické posloupnosti řádu k. Pochybuju o tom ale, takže dle výkladu na jeho škole bych raději odpověděl, že se nejedná o aritmetickou posloupnost (dodejme pro nás na fóru 1. řádu).
daná rekurentně jako výše, je tedy aritmetickou posloupností druhého řádu. Těžko říci, co Karol studuje a jestli je na jeho SŠ obeznámen s pojmem aritmetické posloupnosti řádu k. Pochybuju o tom ale, takže dle výkladu na jeho škole bych raději odpověděl, že se nejedná o aritmetickou posloupnost (dodejme pro nás na fóru 1. řádu).
A ještě poznámka k ↑ ttopimu:. Výpočet členů posloupnosti má špatně. Vyjadřoval jsem se ve svém minulém příspěvku k "mixování" konkrétních hodnot a proměnných. Je jasné, že je tam chyba. Výsledek od Cheopa v příspěvku #5 je správný a zachycuje tvoření členů číselné posloupnosti rekurentně dané. Myslím, že to vystihnul velice dobře a není třeba dalšího komentáře.
U ttopiho pak vidím de facto dvě situace. Buď se spletl, nebo nepochopil smysl tvoření členů číselné posloupnosti rekurentně dané. Nechme ho se k tomu vyjádřit.
Relativně snadno se dá pak ukázat, že platí  .
.
Offline
#7 11. 08. 2008 17:01
Re: Posloupnosti
Předem musím říct, že jsem nad tím hodně přemýšlel, protože původně jsem měl výpočet jako Cheop (ten správný).
Pak mě ale zarazilo, že tazatel uvádí výsledek, tak jsem myslel, že má být správný. Možné je také to, že správný je a je trošku jinak napsáno zadání.
oo^0 = 1
Offline
#8 11. 08. 2008 17:25 — Editoval Marian (11. 08. 2008 17:25)
Re: Posloupnosti
↑ ttopi:
Podle toho, co píšeš ve svém prvním příspěvku, soudím, že akceptuješ  . Pak musíš také akceptovat, že je
. Pak musíš také akceptovat, že je 
Tedy jak jsem psal, posloupnost rozdílů  je posloupnost aritmetická, nicméně tvůj výpočet nedává tento výsledek. Zkus si to pro své rozdíly.
je posloupnost aritmetická, nicméně tvůj výpočet nedává tento výsledek. Zkus si to pro své rozdíly.
Je nyní na autorovi (tazateli), jestli jsme to trefili. Pokud nikoliv, je zapotřebí ještě diskutovat.
Offline
#10 11. 08. 2008 18:12 — Editoval Marian (11. 08. 2008 18:13)
Re: Posloupnosti
Ale posloupnost jejich rozdílů už ano. Podle zadání, pokud jej akceptujeme stejně jako jsme to činili až do teď, je jasné, že hledaná posloupnost je taková, že posloupnost rozdílů a_{n+1}-a_{n} je aritmetická. Tomu ale nevyhovuje výsledek Karola ani tvůj, tedy vámi nalezené členy hledané posloupnosti nemohou být správně. Chtěl jse jen nějak snadno ukázat, že nemá Karol pravdu. Ty také nemáš v tom příspěvku pravdu, ale už jsi psal, že jsi to vypočítal správně (podobně jako Cheop v #5).
Offline
#11 11. 08. 2008 18:17 — Editoval jelena (11. 08. 2008 18:18)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Posloupnosti
↑ Cheop:, ↑ Marian:, ↑ ttopi:
Zdravím vás :-)
Já se přimlouvám za překlep buď v zadaní nebo ve vysledku, respektivě, že to k sebe nesedí :-)
Posloupnost -1, 4, 11, 20, 31 je pěkná, opravdu každý další člen (počínaje 2. členem) vzníka z předchozího přičtením (2n+1). Zřejmě to autor zadání tak nějak viděl, ale trochu dozmatkoval.
Posloupnost zadana jako  - to je ta posloupnost rozdílů, jak říká Marian, je také pěkná:
- to je ta posloupnost rozdílů, jak říká Marian, je také pěkná:
3, 5, 7 ... a je aritmetická.
Pěkně je také tady :-)
A docela pěkný zmatek z vás musí mít kolegYNĚ Karol, která nám říkala, že se připravuje na přijímačky do Plzně. Tak ji nějak uklidnete :-)
Už jsem kibicovala dost :-) a odcházím žehlit :-)
Offline
#14 11. 08. 2008 19:07
Re: Posloupnosti
Tím se potvrzuje můj předpoklad. A sice, že to první n patří předchozímu členu a tedy a_n je hodnota předchozího členu a to druhé n patří právě počítanému členu, tedy n=2 (hned na začátku), pak jsou moje výpočty podle řešení správně.
Samozřejmě že je to tak špatně, proto mě to také zaskočilo.
Chyba bued tedy buď v zápisu, nemůžeme ale vyloučit ani chybu autora testů, nikdo není neomylný. Zkrátka se spletl a počítal to stejně jako já s Cheopem.
oo^0 = 1
Offline
#17 11. 08. 2008 19:30 — Editoval jelena (11. 08. 2008 19:35)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Posloupnosti
↑ ttopi:
Jsem tuto důležitou informaci hlasila před hodinou, kolego :-)
↑ Karol:
Zdravím :-) nemáš nějaké jiné zadání na posloupnosti (ze stejné přípravy na přijimačky)?? Třeba bychom z toho odvodili sled myšlenek autora zadaní.
Jinak tady na foru by mel být odkaz na sbírku Petakové nebo zde je něco z Plzně :-) - Marian určitě bude mít výhrady k úpravě, ale jako sbírka snad poslouží.
Hodně zdaru :-)
Editace:-) dotaz pro kolegy - tady ještě něco bylo z Plzně http://forum.matweb.cz/viewtopic.php?id=2640 - pokud máš čas a náladu, můžete se vyjádřit v původním tématu, jak odkazuji (je to z přijímaček pro rok 2007/2008. Děkuji :-)
Offline
#18 11. 08. 2008 19:51
Re: Posloupnosti
↑ jelena:
dík,mám další příklady,ale jsou trochu jinak postavený,ale asi dost podobný:
Posloupnost je daná vzorcrm pro n-tý člen an = 2n + 1 nebo stejné zadání an= 3n + 5n(na druhou..)
a) napišt prvních pět člrnů
b)graf
c)rozhodnout o jakou posl. se jedná a zdůvodnit
řešení: a) 3, 5, 7, 9, rostoucí aritmetická s d = 2 8 ,26 ,54, 92, 140..., neni to ani arit ani geom...
Offline
#19 11. 08. 2008 20:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Posloupnosti
↑ Karol:
To je jednodušší varianta - pokud se podivaš do materiálu Posloupnost, na který se odkazuji, tak je to vysvětlěno dost názorně:
an = 2n + 1
a) napišt prvních pět členů - za n budeme postupně dosazovat 1, 2, 3, 4, 5
dostaneme:
a_1 = 2*1 +1 = 3
a_2 = 2*2 +1 = 5
a_3 = 2*3 +1 = 7
atd. posloupnost prvních 5 členů bude 3, 5, 7, 9, 11
b) graf - budou to samostané body - na ose x bude 1, 2, 3, 4, 5 na ose y budou hodnoty, co jsme počítali 3, 5, 7, 9, 11 - vzor grafu je v odkazu
c)rozhodnout o jakou posl. se jedná a zdůvodnit - je vidět, že každy člen se liší od předchozího o 2, ale to se musí zdůvodnit obecně:
zapíšeme členy následující  - za n jsem dosadila (n+1) a předchozí, jak jsou za sebou
- za n jsem dosadila (n+1) a předchozí, jak jsou za sebou  . Pokud je posloupnost aritmetická rozdíl těchto členů musí být číslo (žádný výraz obsahující n):
. Pokud je posloupnost aritmetická rozdíl těchto členů musí být číslo (žádný výraz obsahující n): a máme d. Mohli bychom ještě ověřit, zda není geometrická - podíl členu by vychazelo číslo (opět ve výsledku dělení následujícího a předchozího členů nesmí být n) - můžeš to zkusit, nebude geometrická.
a máme d. Mohli bychom ještě ověřit, zda není geometrická - podíl členu by vychazelo číslo (opět ve výsledku dělení následujícího a předchozího členů nesmí být n) - můžeš to zkusit, nebude geometrická.
Doufám, že se objeví online kolega ↑ ttopi:, poprosím ho, a? dál dohlíží a už teď mu za to děkuji :-)
Napíš třeba, co si myslíš o 2. zadání. OK
Offline
#21 11. 08. 2008 20:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Posloupnosti
↑ Karol:
Na procvičení rekurentního vzorce zkus upravenou variantu tveho zadani:
Posloupnost je dána rekurentně:
a1 = -1
a)napiště prvních pět členů
b)načrtněte graf posloup.
c) Rozhodněte, zda se jedná o posl. arit. nebo geom..
řešení: -1, 4, 11, 20, 31, 44
rostoucí posloupnost
není ani arit ani geom...
Offline
#23 12. 08. 2008 00:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Posloupnosti
↑ Karol:
Kdo řikal, že blbě?
↑ Cheop: - příspěvek č. 5 - určitě správně (že ten výsledek nesedí s autorem, za to muže autor, ne Cheop :-)
U jiných příspěvků - je to spíše debata k tomu, co vlastně autor zadání myslel a proč nemyslel něco jiného (a to my samozřejmě nevíme :-)
(je nutné si uvedomít, že pokud nějaký prvek má pořádí n, tak je to jeho jedinečná pozice - následující prvek půjde na pozici (n+1), předchozi na (n-1), nemůžeme říkat, že jedno n je takové a druhé n je nějaké jiné).
Pokud máš zájem, tak sem napíš svůj výpočet ke kontrole, hodně zdaru :-)
Offline



