Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 12. 2011 17:11
Logaritmické rovnice
Ahoj, štve mě pár logaritmických rovnic. Už mi začíná hrabat z toho, jak mi to furt nevychází.
Vážně jsem se snažila, ale vždycky zamrznu na nějakém mrtvém bodě, tzn. odstraním zlomky a nevím, jak dál. Pomůžete? :)
Děkuji předem :)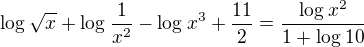
Offline
- (téma jako vyřešené označil(a) Žárovka)
#2 11. 12. 2011 17:15 — Editoval ((:-)) (11. 12. 2011 17:16)
Re: Logaritmické rovnice
↑ Žárovka:
1. Poprosím do jednej témy jednu úlohu, presne podľa pravidiel.
2. Akú úpravu okrem násobenia menovateľom si urobila v 1. úlohe?
Treba použiť vlastnosti logaritmov - napríklad 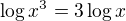 alebo
alebo 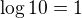 a ďalej aj vlastnosti mocnín, napríklad
a ďalej aj vlastnosti mocnín, napríklad 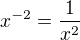
Offline
#4 11. 12. 2011 17:22
- marnes

- Příspěvky: 11227
Re: Logaritmické rovnice
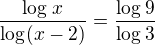
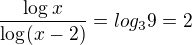
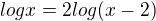
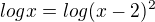
zbytek už zvládneš
Jo. A na začátku vás zdravím.
Offline
#6 11. 12. 2011 17:26
- marnes

- Příspěvky: 11227
Re: Logaritmické rovnice
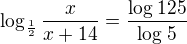
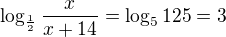
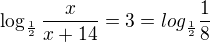
zbytek zvládneš
Jo. A na začátku vás zdravím.
Offline
#8 11. 12. 2011 17:30
- marnes

- Příspěvky: 11227
Re: Logaritmické rovnice
↑ Žárovka:
To chce trénovat:-) začátky jsou těžké, pak už to půjde samo, uvidíš
Jo. A na začátku vás zdravím.
Offline