Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 12. 2011 14:02
Limity
Dobré odpoledne, prosím o kontrolu 2 limit.
1)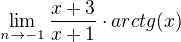
Dosadím, zjístím že to je 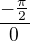
oboustranná liimta neexistuje a budu vyšetřovat jednostranné limity.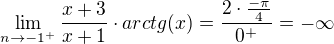
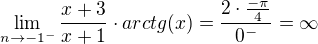
Výsledek by měl být správně(podle Wolframu), jde mi spíš o to, jestli je to jedostatečně odůvodněné, když to takhle napíšu do písemky.
2)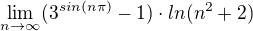
Takže je to typ 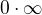 a normálně bych se ho snažil převést na
a normálně bych se ho snažil převést na  nebo
nebo  a pak l'Hopitalem, ale tady jsou ty derivace nějaké podivné a spíš se mi zdá, že to zhoršují.
a pak l'Hopitalem, ale tady jsou ty derivace nějaké podivné a spíš se mi zdá, že to zhoršují.
Wolfram moc nepomohl, nejspíš proto, že nevím jak mu zadat že to je limita posloupnosti.
Díky za pomoc.
Offline
- (téma jako vyřešené označil(a) Crusad)
#2 31. 12. 2011 14:09
Re: Limity
Dosadím, zjístím že to je
oboustranná liimta neexistuje a budu vyšetřovat jednostranné limity.
To je irelevantní. bod x = -1 nikde nevystupuje.
Jednostranné limity jsou správně. To, že si nejsou rovny implikuje neexistenci oboustranné limity.
Ad 2)
Zkoumej zvlášť n sudé a n liché nebo tak nějak to zkus rozdělit. Využij pak to, co víš o podposloupnostech a jejích limitách.
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 31. 12. 2011 14:20
- Marbulinek

- Příspěvky: 33
- Reputace: 0
- Web
Re: Limity
1) Môžeš vychádzať z definície limity, teda limita existuje len vtedy, ak existujú jej jednostranné limity a sú rovnaké..
2) Limitu typu 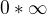 skús previesť na tvar
skús previesť na tvar ![kopírovat do textarea $\lim_{n\to \infty }f(x)g(x) = \lim_{n\to \infty }\frac{g'(x)}{[\frac{1}{f(x)}]'}$](/mathtex/71/71030a7b8c697ec52c4a5f362945a295.gif) a upraviť ;)
a upraviť ;)
"Polib si elipsy"
Offline
#4 31. 12. 2011 14:31
Re: Limity
↑ Marbulinek:
Co bude mít z úpravy, kterou navrhuješ?
What does a drowning number theorist say?
'log log log log ...'
Offline
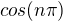 a to se mi nezdá jako zjednodušení situace.
a to se mi nezdá jako zjednodušení situace.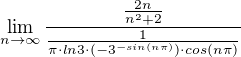
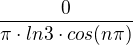 a co s tím dál - respektive je to tedy 0?
a co s tím dál - respektive je to tedy 0?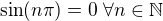 ?
?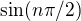 .
.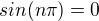 podle mě vždycky, takže rozdělovat na sudé a liché n nemá smysl.
podle mě vždycky, takže rozdělovat na sudé a liché n nemá smysl.