Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 12. 2011 21:57
odporová síla vzduchu na těleso
Těleso o hmotnosti 800 g padající z výšky 17m dopadlo na zem za 3s. Určete odporovou sílu , kterou vzduch působil na padající těleso. Předpokládejte, že odporová síla byla po celou dobu pádu stejná. g=10m/s2, výsledek odporové síly má být 4,98N. Děkuji za pomoc :-)
Offline
- (téma jako vyřešené označil(a) mufik)
#2 01. 01. 2012 11:42 — Editoval TomDlask (01. 01. 2012 11:43)
Re: odporová síla vzduchu na těleso
Zdravím, odporová síla působí proti směru síly gravitační, platí tedy:
( je výsledná síla,
je výsledná síla,  je odporová,
je odporová, 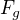 je gravitační)
je gravitační)
Dále víme, že se jednalo o pohyb zrychlený, pro který bude platit 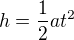 , kde
, kde  je výška,
je výška,  je zrychlení a
je zrychlení a  je doba pádu.
je doba pádu.
Druhý Newtonův zákon nám zase říká, že pro 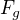 ,
,  a
a  platí:
platí: 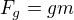 , obdobně platí i pro
, obdobně platí i pro  ,
,  a
a  následující:
následující: 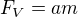
Z těchto vztahů získáme: (dosazeno za
(dosazeno za  )
)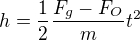 (dosazeno za
(dosazeno za  )
) (dosazeno za
(dosazeno za 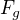 )
)
Nyní stačí již jen vyjádřit 

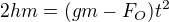

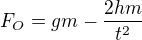
Již stačí jen dosadit.
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline

