Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 01. 2012 16:51
Exponencionální rovnice
Mám exponencionální rovnici, kde nevím, jak upravit jeden člen, tím pádem se nemůžu dostat ani k té základní úpravě. :( Prosím o radu.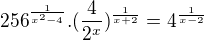
Takže jsem se dostala jen k tomuhle: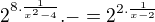
Prosím poraďte mi..
Offline
- (téma jako vyřešené označil(a) zuzule1)
#3 01. 01. 2012 17:07 — Editoval vanok (01. 01. 2012 17:12)
Re: Exponencionální rovnice
Ahoj ↑ zuzule1:,
Uprav to na tuto formu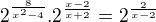
a potom 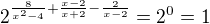
A na koniec podla vlasnosti mocnin, vyries
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 01. 01. 2012 17:13
Re: Exponencionální rovnice
↑ TomDlask: děkuju za radu, zkusím to dopočítat. :) Akorát bych se ráda zeptala, jak se zbavím toho zlomku..??
Offline
#5 01. 01. 2012 17:22
Re: Exponencionální rovnice
↑ zuzule1:
Dále bych postupoval takto: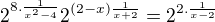


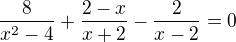
Převést na společného jmenovatele
Vynásobit jmenovatelem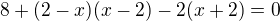
A nemáme žádné zlomky.
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline
#6 01. 01. 2012 17:31 — Editoval vanok (01. 01. 2012 17:32)
Re: Exponencionální rovnice
Ahoj ↑ TomDlask:;
To nasobenie mozes urobit, ale za podmienky ze 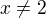 ako aj
ako aj 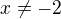
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 01. 01. 2012 17:32
Re: Exponencionální rovnice
↑ TomDlask: Já se omlouvám, špatně jsem napsala otázku. Ano, tenhle postup zvládám, děkuju. Já myslela jak se zbavím zlomku v tomhle kroku: 
Offline
#8 01. 01. 2012 17:34
Re: Exponencionální rovnice
↑ zuzule1: Omlouvám se za tak blbej dotaz, ale úpravy nikdy nebyla moje silná stránka. :)
Offline
#9 01. 01. 2012 17:52
Re: Exponencionální rovnice
↑ vanok: Ano, to jsem předpokládal, protože již v zadání je ve jmenovateli 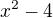 takže platí ty podmínky, co jsi napsal, díky za upřesnění.
takže platí ty podmínky, co jsi napsal, díky za upřesnění.
↑ zuzule1: Použil jsem pravidlo  (pro
(pro  )
)
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline