Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spektrální rozklad (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 01. 2012 22:31
Spektrální rozklad
Zdravím všechny a měl bych pro vás dotaz zde je názorně vypočítaný příklad stránka 71 příklad č. 1. já to chápu jak to vypočítat jediný důvod proč se dál nedostanu je to že nechápu výpočet vlastního čísla. :(
Dosazení čísla lambdy chápu ale to je vše nechápu když si dosadím do matice lambdu co pak mám dál dělat byl bych rád za vysvětlení děkuji :)
http://dl.dropbox.com/u/2327863/LAIT/Cviceni/lacv14.pdf
Offline
- (téma jako vyřešené označil(a) georgeo4)
#2 01. 01. 2012 22:41
Re: Spektrální rozklad
Ahoj ↑ georgeo4:,
Mozno nevidis, ze
Pisat 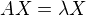 je equivalentne z
je equivalentne z 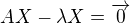
a vlastne toto je pouzite v tvojom texte pre kazdu vlastnu hodnotu
Staci?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#3 01. 01. 2012 22:58
Re: Spektrální rozklad
↑ vanok:
Bohužel asi nestačí :)
Jo tu definici chápu tohle vysvětlit je těžké pro tebe abych to pochopil.
Mě by pomohl kdybys třeba napsal jednoduchou matici a napsal to dosazení lambdy a vypočet vlastnhío čísla ale to by bylo asi na dlouho že ? No kdyžtak to zkusím nějak na to přijít sám jinak díky teda :)
Offline
#4 01. 01. 2012 23:00
Re: Spektrální rozklad
↑ georgeo4:,
Tan prepis na matricovu formu chapes?
Tam autor potom pouzije Gausovu metodu na riesenie kazdej z rovnic.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#6 01. 01. 2012 23:07
Re: Spektrální rozklad
↑ georgeo4:,
ano vlastne hodnoty to je po vypocitani det. riesenie rovnice... tu je jednocha na vyriesenie.
Potom rie tri systemy to je na hladanie ( Gauss-ovov eliminacnou metodou) hladanie vlastych vektorov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#7 01. 01. 2012 23:09
Re: Spektrální rozklad
Pozri aj sem http://cs.wikipedia.org/wiki/Vlastn%C3% … D%C3%ADslo
su tam aj priklady.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#8 01. 01. 2012 23:15
Re: Spektrální rozklad
↑ georgeo4:,
Po dosadeni do"matice" 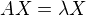 napriklad
napriklad  to je ten prvy pripad
to je ten prvy pripad
das vsetko na jednu stranu ( nezname su na pravo potom) tri nezname, su zlozky vlastneho vektoru
( POZOR vlastne hodnoty uz mas a ...to co si pisal↑ georgeo4:je nepresne )
To riesenie od autora toho prveho systemu chapes?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#9 01. 01. 2012 23:23
Re: Spektrální rozklad
↑ vanok:
Bude to semnou těžké asi to dělá to že už je tolik hodin
Jak jsi mi poslal ten odkaz tak jak je ten vzorový příklad matice dole Je tam charakteristická rovnice do té matice se dosadila lambda a potom už nevím tu operaci nebo co udělal že má
kvadratickou rovnici lambda^2 -3lambda + 2 ? :(
Offline
#10 01. 01. 2012 23:33 — Editoval vanok (01. 01. 2012 23:35)
Re: Spektrální rozklad
↑ georgeo4:,
No to tam vypocital determinant
det | a b|
| c d|
kde 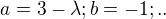 atd...
atd...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#11 01. 01. 2012 23:37
Re: Spektrální rozklad
no ja idem spat, zajtra len co budem moct pozrem ako si na tom a odpoviem. bye
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#12 02. 01. 2012 08:28 — Editoval georgeo4 (02. 01. 2012 09:32)
Re: Spektrální rozklad
Myslím že jsem to pochopil tak kvadratická rovnice vznikla tak, že 3-lambda * - lambda -(-1)*2 ? u toho tvojeho příkladu z odkazu.
A tedy jestliže mám já takovou matici dosadíl jsem lambdy a udělal to podobně jako u toho příkladu v prvním odkazu jen jestli to mám dobře ? :) A jestli to chápu dobře k těm vlastním číslům dojdu tak, že vypočítám determinant matice ? :)
Myslím si že když mám tady tenhle příklad že už je to dobře :)
Já si připsal pod matici první dva řádky a udělal nedopočítaný determinant je to dobře ne ? :)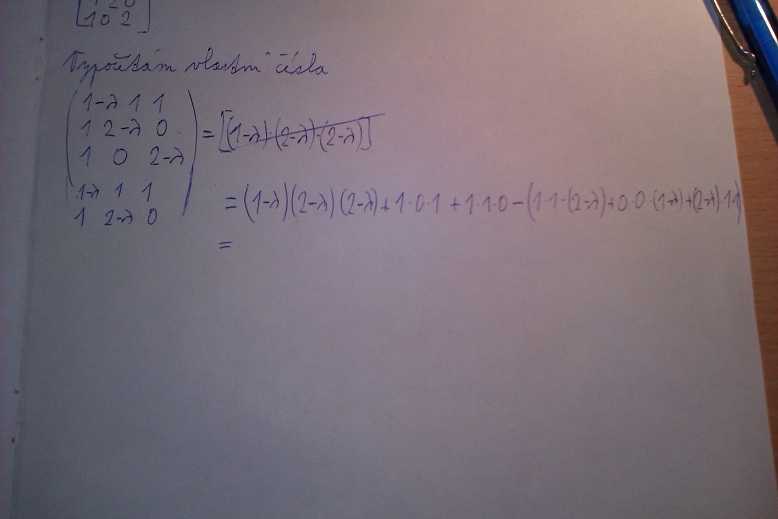
??
Offline
#13 02. 01. 2012 09:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad
↑ georgeo4:
Zdravím,
speciálně pro spektrální rozklady máme téma - druhé úvodní, má se číst před vložením dotazu do sekce VŠ. Minimální užitek tohoto tématu je šablona pro vložení zápisu v TeX (místo luštění ruční nečitelné tvorby). Jinak doporučuji si nastudovat pravila výpočtu determinantů.
Pokud neuvidím slušné zápisy, tak téma zamknu.
↑ vanok: omlouva za vstup, věřím, že bude k užitku v tématu. Zdravím.
Jelena
Offline
#14 02. 01. 2012 09:42 — Editoval vanok (02. 01. 2012 09:54)
Re: Spektrální rozklad
↑ georgeo4:,
Nie.
Chcel si ako v tvojom materialy rozvinut podla prveho riadku.
V tvojom materiali v tom riadku su dve nuly a tak u neho staci pocitat len jeden Laplac-ov kofaktor.
a u teba treba dva.
TVOJ PROBLEM SU ASI DETERMINANTY
Jedna dolezita vec AUTOR tvojho textu predpoklada dokonalu znalost determinantov.
Napis mi tu co vies o rozvoje determinantu podla jedneho riadku ( cf: Laplace-ova metoda)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#15 02. 01. 2012 09:52
Re: Spektrální rozklad
Ahoj ↑ jelena:,
Vsetko najlepsie do noveho roku 2012.
Ano mas pravdu ze material na ktory odkazujes by mal povinne citat kazdy co ma problemy z takouto tematikou. Je to jeden z pedagockych pristupou k veci.
Citat bez poznania abecedy, alebo robit priklady bez znalosti teorie nedokaze ani genius!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#17 02. 01. 2012 10:07
Re: Spektrální rozklad
↑ georgeo4:,
Co vlastne studujes?
Kolegina ti dala cestu kde sa to mozes naucit ↑ jelena:
Ale podla tvojho materialu... taketo metody musia byt asimilovane!
Inac sa budes len motat dokola a kazda neznalost ta zastavi... mozno existuju aj ine materialy co by ti mohli pomoct. Napis koleginy tu ci ti moze v tom poradit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
#18 02. 01. 2012 10:15
Re: Spektrální rozklad
↑ vanok:
Já jsem na Všb tam kam mě odkázala tak se mi žádné téma nezobrazí.
Já doteď neměl s ničím žádný problém pochopit.
Tedkom prostě nevím to že když mám matici 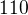
 a počítám spektrální rozklad potřebuji vlastní čísla matice následně vlastní vektory.
a počítám spektrální rozklad potřebuji vlastní čísla matice následně vlastní vektory.
Já nevím jak dojít k těm vlastním číslům to jediné :)
Offline
#19 02. 01. 2012 10:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad
↑ georgeo4:
v tématu pro VŠB je zápis matice v TeX (cca uprostřed textu, ve skrytém textu - rozkliknout, kliknout na zápis, ten se přenese do Tvé zprávy).
Nefunguje odkaz na str. pana Beremlijského - zde kolega od vás zanechál náhradní - funguje?
↑ vanok: děkuji a také všem všechno nejlepší do nového roku.
Offline
#20 02. 01. 2012 10:46 — Editoval georgeo4 (02. 01. 2012 10:48)
Re: Spektrální rozklad
↑ jelena:
Jo to jsem našel a to je právě ten problém já nemůžu prostě pochopit kde třeba vzali (-1)^1+2 ?
Nechápu jak rozvinout determinant :( že se dosadí lambda do matice to vím ale no dejme tomu, že máme tuhle matici:
já bych to udělal takhle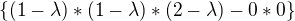
udělal jsem to podle téhle matice:Napsal nám ji sám učitel.
což je 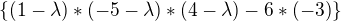 což se rovná závorky +18 ne ? :)
což se rovná závorky +18 ne ? :)
Offline
#21 02. 01. 2012 10:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad
↑ georgeo4:
už je to lepší (co do úpravy), ale Laplace rozvoj si, prosím, ještě dostuduj - odkud je (-1)^(1+2) pokračuj, prosím, zde: "Teď ještě otravná definice Laplaceovy věty"
Offline
#23 02. 01. 2012 11:04
Re: Spektrální rozklad
↑ georgeo4:,
Ja nesudim ci si mal problemy alebo nie.
Ale mas medzery co musis doplnit.
V tomto pripade ide o determinanty tak ako su pouzite v materialy co si napisal vysie↑ georgeo4:.
Otazky co si mi dal som ti trpezlivo vysvetlil... a tvoje otazky mi dokazuju ze musis doplnit tvoje slabe body...
Tak najprv prestuduj tie materialy co su tu k dispozicii .... a osvoj aj laplace-ovu metodu co je pouzita v tvojom materialy to mas pravdu ze pre determinanty (3,3) to mozno nie je treba ale tak ci tak AK JE POUZITA V TVOJICH MATERIALOCH AUTOR TEXTU SA TA NA TO MOZE OPYTAT
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Online
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spektrální rozklad (TOTO TÉMA JE VYŘEŠENÉ)
