Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Substituce v diferenciální rovnici (TOTO TÉMA JE VYŘEŠENÉ)
#1 31. 01. 2012 14:13
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Substituce v diferenciální rovnici
Ahoj, řeším následující diferenciální rovnici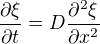
popisující jednorozměrnou difuzi, řešením je tedy funkce dvou proměnných - času a jedné souřadnice. Aby bylo možné použít analogii mezi difuzí a vedením tepla a následně teorii podobnosti, zavede se substituce vedoucí na bezrozměrné veličiny:
 ,
,  ,
,  . Tyto výrazy se dosadí do rovnice a má vyjít:
. Tyto výrazy se dosadí do rovnice a má vyjít: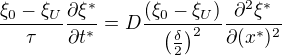 , po úpravě
, po úpravě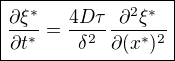 .
.Kdyby byla
 funkce jedné proměnné, tak by se dalo psát
funkce jedné proměnné, tak by se dalo psát  , což se nějak dosadí do původní rovnice. Tady by se to asi mělo značit jinak...? Tohle ale ještě docela chápu, problém mám spíš s tou druhou derivací - kde se vzalo
, což se nějak dosadí do původní rovnice. Tady by se to asi mělo značit jinak...? Tohle ale ještě docela chápu, problém mám spíš s tou druhou derivací - kde se vzalo 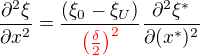 ? Díky za rady.
? Díky za rady. Offline
- (téma jako vyřešené označil(a) FliegenderZirkus)
#2 31. 01. 2012 14:30 — Editoval Pavel Brožek (31. 01. 2012 14:32)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Substituce v diferenciální rovnici
↑ FliegenderZirkus:
Odtud: .
.
(Jde vlastně o derivaci složené funkce.)
Offline
#3 31. 01. 2012 15:27
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Substituce v diferenciální rovnici
↑ Pavel Brožek:
Jasně, analogicky pak tedy bude: 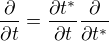 ,
, . Asi už rozumím, ale možná ještě přibyde jeden dotaz, proto zatím za vyřešené neoznačím. Díky.
. Asi už rozumím, ale možná ještě přibyde jeden dotaz, proto zatím za vyřešené neoznačím. Díky.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Substituce v diferenciální rovnici (TOTO TÉMA JE VYŘEŠENÉ)
 ,
, 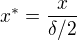 ,
, 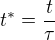 , kde význam těch koeficientů teď není důležitý. Po vyjádření:
, kde význam těch koeficientů teď není důležitý. Po vyjádření: