Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#27 28. 10. 2008 19:52
Re: slovni ulohy
už půl hodiny si lámu hlavu s na prví pohled lehkým příkladem: Hlediste kina o kapacitě 500 míst je rozděleno do řad o stejném počtu křesel. po rekonstrukci se jeho kapacita snížila o 10 procent. pět řad ubylo, zato v každé řadě přibylo 5 křesel.Kolik řad mělo původní hlediště?
nevím rovnici a i kdybyh ji věděl tak to takm asi nedosadím. prosím o vypočtení a vysvětlení. předem děkuji.
Offline
#28 28. 10. 2008 20:01
Re: slovni ulohy
↑ martas277:
x*y = 500
(x + 5)*(y-5) = 0,9*500
x...pocet sedadel v rade
y...pocet rad
Matematika je jednoduchá, záleží pouze na úhlu pohledu.
Offline
#29 29. 10. 2008 06:47
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovni ulohy
↑↑ martas277:
Šlo by to počítat i takto:
Označme x - výkon čerpqadla při napouštění (m^3/min)
Pak platí:
Nikdo není dokonalý
Offline
#30 29. 10. 2008 11:03
Re: slovni ulohy
potřboval bych pomoc s touto úlohou:Obdélník má pětkrát větší délku než šířku. Zmenšíme-li oba jeho rozměry o 4cm, dostaneme obdélník, jehož obsah je roven 55,2%obsahu původního obdélníku. Určete, kolik procent obvodu původního obdélní je obvod obdélníku zmenšeného.
řešil jsem: 0,552y=[(x*5)-4]*(x-4) ale to je asi nesmysl
prosím vypočítat a vysvětlit. Předem děkuji.
Offline
#31 29. 10. 2008 11:58 — Editoval matoxy (29. 10. 2008 12:00)
Re: slovni ulohy
Prvý obdĺžnik má strany  ,
, 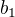 , ktoré sú v pomere 1:5. Čiže
, ktoré sú v pomere 1:5. Čiže  ,
, 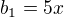 . Jeho obsah označme
. Jeho obsah označme 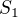 a vypočítame ho
a vypočítame ho 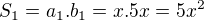 . Obsah obdĺžnika, ktorý má strany kratčšie o 4 cm označíme
. Obsah obdĺžnika, ktorý má strany kratčšie o 4 cm označíme  .
.
Pre obsahy tiež platí:  .
.
Vedel by si to ďalej dopočíta??
You know who
(or maybe not)
Offline
#33 29. 10. 2008 12:04 — Editoval Cheop (29. 10. 2008 14:07)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovni ulohy
↑ martas277:
Označíme x - šířka původního obdélníku
5x - délka pův. obdélníka
Obsah původního obdélníka je: 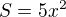
Zmenšený obdélník má obsah 55,2 % původního tj: 
Obsah zmenšeného obdélníka tedy bude: - úpravou dospějeme ke kvadratické rovnici:
- úpravou dospějeme ke kvadratické rovnici:
Tedy šířka původního obdélníka je 10 cm a jeho délka pak 5 krát větší tj: 50 cm.
Obvod původního obdélníka je:
Obvod zmenšeného obdélníka je:
Procento tedy bude:
Obvod zmenšeného obdélníka bude přibližně 86,7 % obdélníka původního.
Nikdo není dokonalý
Offline
#35 04. 11. 2008 14:19
Re: slovni ulohy
potřeboval bych poradit s tímto příkladem: V první krejčovské dílně měli ušít 810 obleků, ve druhé dílně měli za stejné období ušít 900 obleků. První dílna splnila úkol 3 dny před termínem, druhá 6 dnů před termínem. Kolik obleků ušili průměrně denně v první dílně, bylo-li to o 21 obleků méně než ve druhé dílně?
Offline
#37 04. 11. 2008 15:27
Re: slovni ulohy
Vím, že to tu nemají rádi, ale pomohu si vzorečkem 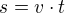 , tedy vzorečkem pro dráhu, což v tomto příkladu zastupuje počet ušitých obleků.
, tedy vzorečkem pro dráhu, což v tomto příkladu zastupuje počet ušitých obleků.
Co vím: první dílně udělají o 21 obleků za den méně.
první dílně udělají o 21 obleků za den méně. - rychlostí
- rychlostí  ušijí za x dní 900 obleků.
ušijí za x dní 900 obleků.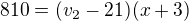 v první dílně dělají o 3 dny déle.
v první dílně dělají o 3 dny déle.
Dostávám soustavu rovnic. Vyjádřím si třeba z 1.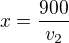 a dosadím do 2. rovnice
a dosadím do 2. rovnice
Takže první dílna pracovala 15 dní a za den ušila 54 obleků. Druhá dílna pracovala 12 dní a za den ušila 75 obleků.
oo^0 = 1
Offline
#38 05. 11. 2008 08:22 — Editoval Cheop (05. 11. 2008 10:18)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovni ulohy
↑ ttopi:
My, co nemáme rádi míchat slovní úlohy o pohybu se slovními úlohami
o společné práci bychom to řešili následovně:
Označme: x - denní výkon první dílny
x+21 - denní výkon druhé dílny
Pak lze ze zadání sestavit rovnici: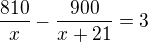 -úpravou (první dílna pracovala o 3 dny déle než druhá)
-úpravou (první dílna pracovala o 3 dny déle než druhá)
Denní výkon druhé dílny je 
V první dílně ušijí denně 54 obleky ve druhé pak 75 obleků.
EDIT: Tím Tvůj výpočet nijak nekritizuji jen se mi ten můj zdá takový přehlednější.
Trochu obtížnější by byla úloha v případě kdyby otázka zněla:
Kolik obleků denně ušíjí v první dílně při původním výkonu?
Nikdo není dokonalý
Offline
#39 06. 11. 2008 00:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovni ulohy
↑ ttopi:, ↑ Cheop:
Zdravím vás :-)
My, co máme nejraděj směsí, tvrdime, že oba používate stejný přístup - přímou uměru "celkového výsledku" a "výsledku za jednotku času" (rychlost, produktivita apod.) Jen kolega ttopi zapisuje úměru rovnou jako "výsledek" a kolega Cheop - vyjadřuje z "výsledku" čas, potřebný na jeho dosažení.
Abychom z tohoto zadaní vyrobili úlohu o společné práci, musela by byt nějak upravena, aby se porovnaval stejný výsledek. Ale teď nemám nějaký nápad :-)
V každém případě jsem velký odpůrce zařazení slovních úloh do škatulek, ale bohužel praxe je taková, že je problém naučit řešit i pomocí škatulek - a tento problém se každým rokem prohlubuje - nevím proč tomu tak je.
Už jsem dokonce slyšela zařazení slovních úloh do typů "a to je úloha na dělení nebo na násobení", ach jo :-(
Zatim jsem nenašla český text knihy Polya How to solve it velmi doporučuji :-)
-----------------
Jelikož kolegovi ttopi občas hlasim, co pravě poslouchám - tak tedy: So ends another day
a zdravím :-)
Offline
#40 06. 11. 2008 07:17
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovni ulohy
↑ jelena:
Zdravím :)
Máš naprostou pravdu, že slovní úloha je slovní úloha a to je také
jediná kategorie. Mám dojem, že ve škole opravdu upouštějí od řešení
tohoto typu úloh, což je ale velká škoda. Možná by nám k tomu mohla
více říci paní Ivana.
Nikdo není dokonalý
Offline
#41 06. 11. 2008 17:40
Re: slovni ulohy
↑ Cheop:↑ jelena:
Zdravím vás ,
abych se přiznala nad předešlou úlohou mi trochu zůstal rozum stát. Jednak bych řekla, že její zadání je trochu nesrozumitelné; pak jsem dále tápala nad tím, zda jde o úlohu s jednou či dvěma neznámými.
Tak jak úlohu řešil ↑ ttopi: bych ji určitě neřešila a myslím , že mezi žáky bych způsobila paniku. Tedy alespoň v těch žácích, kteří by ji opravdu chtěli poctivě řešit.
A dále , co ta kvadratická rovnice v listopadu školního roku , byt´ v devátém ročníku ?
No a protože v současné době je v našem základním školství docela pěkný chaos , je pak docela možné, že se takové úlohy, kde se neznámá dostává do kvadrátu, i řeší (vyjímkou jsou ty úlohy, kde se neznámá, povýšená na druhou, objeví na obou stranách rovnice, to je pak jiná). Já osobně jsem se s tím nesetkala.
Nakonec bych podotkla, že na slovní úlohy opravdu nezbývá v hodinách času, a berou se v podstatě velmi poskrovnu. Což je velká škoda, nebot´ takového toho selského rozumu mezi žáky ubývá. :-(
Co se týká kategorie - přikláním se ke kategorii "slovní úlohy", bez přívlastků na dělení, na násobení a tak podobně.
Podotýkám, je to můj názor a možná, že se mýlím. :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#42 08. 11. 2008 23:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovni ulohy
↑ Ivana:, ↑ ttopi:, ↑ Cheop:
zdravím vás velmi srdečně a Ivanu moc prosím, aby vyřídila náš pozdrav z Opavy také Zdeňkovi :-)
K samotnému postupu kolegy ttopi nemám výhrady - pouze k tomu, že, pokud je obecně zavedeno nějaké označení, není vhodné ho používat v jiném vztahu (i v případě, že dobře vyjadřuje smysl procesu).
A také vím, že použití dolních indexů u písmen je další problém.
Ale tento postup také používam - pokud řešíme slovní úlohu a nějak se nedaří dostat k rovnici, tak navrhnu, že budeme předpokládat, že je vše známo a vytvoříme zápis vztahů mezi zadanými veličinami. Tak nenásilně dotlačím k zjištění, že je to třeba příma úměra.
Pak do vztahu dosazujeme to, co máme a kontrolujeme, co je úplně neznámo a co můžeme odvodit ze zadaní. A zde se snažím, aby vztahy byly maximálně jednoduché (třeba, pokud se mohu vyhnout patrovému zlomku, tak se vyhnu :-)
Kolega ↑ martas277: by možná mohl doplnit, zda to není úloha z víceletého gymnazia - předpoklad kvadrtické rovnice by byl více jistý.
V každém případě selskému rozumu zdar (zítra ho budu mocí uplatnit v dostatečně míře při práci na chalupě - něco se dnes nařízovalo :-)
Offline
