Matematické Fórum

Kondr · 09. 10. 2008 15:27

Už tu nějaká podobná byla, ale tahle se mi prostě líbí :)
$\lim_{n\to \infty}\tan((5+2\sqrt{6})^n\pi)$

Olin · 09. 10. 2008 15:38

Tak mám takový dojem, že je to nula. Využívám faktu, že $(5+2\sqrt{6})^n$ má za desetinnou čárkou (n-1) devítek.

Kondr · 09. 10. 2008 18:13

↑ Olin:Ano, to je skoro správné řešení. Nebude jich sice n-1, ale vždy víc jak n/2.

Olin · 09. 10. 2008 18:54

Áha, tak to si akorát špatně pamatuji onu úlohu, která byla velmi podobná :)

Marian · 09. 10. 2008 19:38 — Editoval Marian (09. 10. 2008 20:23)

↑ Olin:↑ Kondr:
Nevidím tady stále důkaz, takže to provedu já.

Protože platí
$1=25-24=5^2-(2\sqrt{6})^2=(5-2\sqrt{6})\cdot (5+2\sqrt{6}),$
máme odtud snadno
$\frac{1}{(5+2\sqrt{6})^n}=\left (5-2\sqrt{6}\right )^n=\sum_{k=0}^{n}{n\choose k}(-1)^k5^{n-k}\cdot\left (2\sqrt{6}\right )^k=\nl =\nosmash\sum_{k=0,\, k\;\mathrm{even}}^{n}\nosmash{n\choose k}5^{n-k}\cdot\left (2\sqrt{6}\right )^k-\nosmash\sum_{k=0,\, k\;\mathrm{odd}}^{n}\nosmash{n\choose k}5^{n-k}\cdot\left (2\sqrt{6}\right )^k,$
přičemž první suma je kladný integer (to je důležité), druhou nemusím specifikovat snad jen tolik, že je to kladné reálné číslo. Protože ale $\lim_{n\to\infty}\frac{1}{(5+2\sqrt{6})^n}=0$ , bude se rozdíl těchto dvou kladných čísel neomezeně blížit nule, což jasně implikuje, že druhá suma (za znaménkem minus) je almost integer.

Dále je
$(5+2\sqrt{6})^n=\nosmash\sum_{k=0,\, k\;\mathrm{even}}^{n}\nosmash{n\choose k}5^{n-k}\cdot\left (2\sqrt{6}\right )^k+\nosmash\sum_{k=0,\, k\;\mathrm{odd}}^{n}\nosmash{n\choose k}5^{n-k}\cdot\left (2\sqrt{6}\right )^k,$
což je podle předchozího almost integer. Odtud je vidět, že výraz $(5+2\sqrt{6})^n\pi$ se s rostoucím n neomezeně blíží celočíselnému násobku Pi. Proto je limita rovna nule.

Kondr · 09. 10. 2008 22:25

Moje řešení bylo skoro identické.

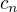V okruhu $\mathbb{Z}[\sqrt{6}]$ jsou čísla $(5+2\sqrt{6})^n$ a $(5-2\sqrt{6})^n$ sdružená, jejich součet je roven nějakému celému číslu $c_n$ . Proto můžeme hledanou limitu upravit do tvaru
$\lim_{n\to \infty}\tan\left(\left(c_n-(5-2\sqrt{6})^n\right)\pi\right)=\lim_{n\to \infty}\tan\left(-(5-2\sqrt{6})^n\pi\right)$ ,
hodnota argumentu se blíží 0, v okolí 0 je funkce tangens spojitá, proto je hledaná limita rovna tan(0)=0.

Matematické Fórum

#1 09. 10. 2008 15:27

Říjnová limita

#2 09. 10. 2008 15:38

Re: Říjnová limita

#3 09. 10. 2008 18:13

Re: Říjnová limita

#4 09. 10. 2008 18:54

Re: Říjnová limita

#5 09. 10. 2008 19:38 — Editoval Marian (09. 10. 2008 20:23)

Re: Říjnová limita

#6 09. 10. 2008 22:25

Re: Říjnová limita

Zápatí