Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Dráha nerovnoměrně zrychleného pohybu (?) (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 02. 2012 23:12
Dráha nerovnoměrně zrychleného pohybu (?)
Zdravím,
rád bych vás poprosil o pomoc. Zajímá mě následující:
Mějme pevnou kladku s lanem, na jednom konci lana závaží o hmotnosti m, na druhém níže pytel s pískem o stejné hmotnosti m (rozdíl výšky pytle a závaží označme h). Po bodnutí nožem do pytle se z něj začne sypat písek s konstantním "výtokem" (jednotka kg/s) a závaží začne klesat (zvedajíc pytel).
Za jakou dobu od bodnutí se budou pytel i závaží nacházet ve stejné výšce?
(Nemám to z žádné sbírky, napadlo mě to při sledování seriálu Sherlock.)
Dokázal jsem si vyjádřit výslednici i zrychlení, ale obojí bylo proměnlivé v závislosti na čase, a z toho jsem nebyl schopen dostat se k rovnici pro dráhu. Když jsem to zkusil přes přeměnu energií (a dost možná že i špatně) stejně jsem tam měl pořád moc neznámých. Tuším, že cesta asi leží v integrálním počtu, ale s tím jsem se začal seznamovat sotva před týdnem, takže...
Předem dík za každou pomoc.
Offline
- (téma jako vyřešené označil(a) Polopat)
#2 09. 02. 2012 20:54
Re: Dráha nerovnoměrně zrychleného pohybu (?)
↑ Polopat: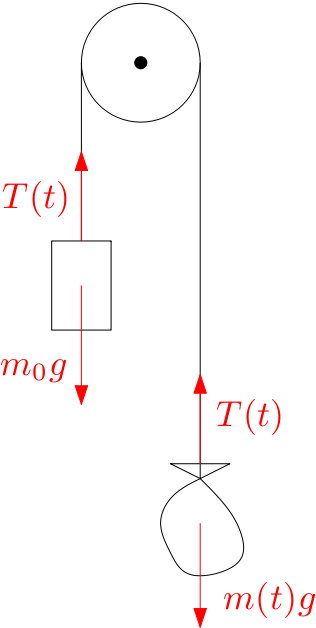
Pokud zanedbáme vliv kladky a tření.
N.Z. pro těleso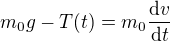 (1)
(1)
pro pytel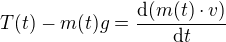 (2)
(2)
kde 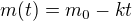 -
-  je ten "výtok"
je ten "výtok"
(1) + (2)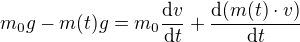
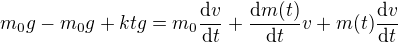 (derivace součinu)
(derivace součinu)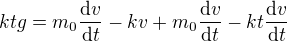
nyní si zavedu parametr  a celou rovnici vydělím
a celou rovnici vydělím  . Dostávám
. Dostávám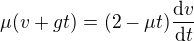
Pokud tě zajímá matematická stránka řešení této difernciální rovnice, zkus to v sekci "Vysoká škola". Já to nechal spočítat stroj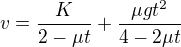 , kde
, kde  je integrační konstanta. Z počátečních podmínek
je integrační konstanta. Z počátečních podmínek 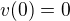 plyne
plyne 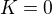 a
a 
Nyní můžeš zjistit zrychlení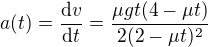
Můžeš taky zjistit např. rychlost v okamžiku, kdy se pytel vyprázdní 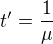 ,
, 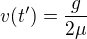
a závislost dráhy na čase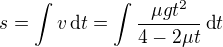
Zase jsem to nechal spočítat stroj![kopírovat do textarea $s=\frac{g}{4\mu ^2}\left[\mu t(\mu t+4)+8\ln \left|\frac{2-\mu t}{2}\right|\right]$](/mathtex/3e/3e4ab780aa80cc69cc0663f472cc5af1.gif) (dráha pytle s už započtenou počáteční podmínkou
(dráha pytle s už započtenou počáteční podmínkou  )
)
Když nyní chceš vědět, kdy se zápaží a pytel potkají, musíš z rovnice![kopírovat do textarea $\frac{g}{4\mu ^2}\left[\mu t(\mu t+4)+8\ln \left|\frac{2-\mu t}{2}\right|\right]=\frac h2$](/mathtex/61/61030c6b1ef3829ea51fc6772982acb9.gif)
vypočítat  . Analyticky to nejde. Smůla.
. Analyticky to nejde. Smůla.
Samozřejmě všechy vztahy platí pouze než se vysype písek.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 12. 02. 2012 16:47
Re: Dráha nerovnoměrně zrychleného pohybu (?)
↑ zdenek1:
Super, děkuju! Nedokázal bych to sice ještě spočítat na papíře bez Wolframu, ale postup už je mi jasný.
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » Dráha nerovnoměrně zrychleného pohybu (?) (TOTO TÉMA JE VYŘEŠENÉ)
