Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » matematická indukce (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 10. 2008 18:18
matematická indukce
Dobrý podvečer,
ač je sobota sedím nad příklady z matematiky a nevím si se 2 příklady jak pokračovat dále (jde o 3. krok .
Prosím o pomoc, pokud bude mít někdo chvilku.
Zadání: dokažte dělitelnost pomocí matematické indukce
př. 1
má úvaha:
př. 2
má úvaha:
dál bohužel netuším, jak to více upravit.
"v Matematice vidím pouhá čísla a žádnou souvislost, potom to tak vypadá :("
Offline
#2 11. 10. 2008 18:44 — Editoval Pavel (11. 10. 2008 18:45)
Re: matematická indukce
Jen pro přesnost, dělitelnost se značí svislou čárkou - příkaz \mid. Dokažme, že vztah platí pro 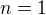 .
. , což je číslo dělitelné 6.
, což je číslo dělitelné 6.
Předpokládejme, že vztah platí pro  , tedy
, tedy  . Dokažme, že platí také pro
. Dokažme, že platí také pro  .
.
Podle indukčního předpokladu je výraz v závorce dělitelný 6 stejně jako číslo 12. Abychom dokázali, že předchozí výraz je dělitelný 6, stačí toto dokázat pro výraz 

Čísla  a
a  jsou dvě po sobě jdoucí přirozená čísla. Tudíž právě jedno z nich musí být sudé. Pak také jejich součin
jsou dvě po sobě jdoucí přirozená čísla. Tudíž právě jedno z nich musí být sudé. Pak také jejich součin  je sudé číslo. Číslo
je sudé číslo. Číslo 
je dělitelné 3 a 2, a tedy 6.
Podobně se postupuje u druhého příkladu.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 11. 10. 2008 22:59 — Editoval lukaszh (11. 10. 2008 22:59)
Re: matematická indukce
U druhého príkladu je to trošku zložitejšie, pretože sa premenná vyskytuje aj v exponente:
Prvý indukčný krok pre n=1 platí pretože 9|9. V druhom kroku ako napísal Pavel predpokladáme, že výrok platí pre n=k, teda 
Pokračujeme v indukcií presne tak ako si napísal a úpravou dostávame:
Vieme zapísa? výraz 7^k+3k-1 v tvare násobku čísla 9, keďže predpokladáme, že je deliteľný číslom 9:
Potom:![kopírovat do textarea $9j+7^k\cdot6+3=9j+(6+1)^k+3=9j+6\cdot\left[{k\choose 0}6^k+{k\choose 1}6^{k-1}+{k\choose2}6^{k-2}\cdots+{k\choose k-1}6+{k\choose k}\right]+3= 9j+6\cdot\left[6^k+k\cdot6^{k-1}+{k\choose2}6^{k-2}\cdots+6k+1\right]+3=\nl =9j+6\cdot\left[(3\cdot2)^k+k\cdot(3\cdot2)^{k-1}+{k\choose2}(3\cdot2)^{k-2}\cdots+(3\cdot2)k\right]+9=9j+18\cdot\left[3^{k-1}\cdot2^k+k\cdot3^{k-2}\cdot2^{k-1}+{k\choose2}3^{k-3}\cdot2^{k-2}\cdots+2k\right]+9 $](/mathtex/6c/6c911f8cb41c22e57a85eaa874118fb1.gif)
Toto je deliteľné deviatimi. Tvrdenie je teda dokázané.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#4 11. 10. 2008 23:28 — Editoval Marian (11. 10. 2008 23:29)
Re: matematická indukce
↑ lukaszh:
Já bych to viděl podstatně jednodušeji, totiž takto.
Pro n=1 je tvrzení snadno ověřitelné (9|9 ... platí). Předpokládejme, že dokazované tvrzení platí pro všechna  taková, že
taková, že  , kde n je fixní přirozené číslo, tj. předpokládejme, že platí
, kde n je fixní přirozené číslo, tj. předpokládejme, že platí
Vyšetřujme nyní výraz  , o kterém máme dokázat za stanovených předpokladů, že je dělitelný devíti (nic snadnějšího ...). Platí totiž
, o kterém máme dokázat za stanovených předpokladů, že je dělitelný devíti (nic snadnějšího ...). Platí totiž
Hotovo!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » matematická indukce (TOTO TÉMA JE VYŘEŠENÉ)

