Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 10. 2008 12:04
- Jakub Pištěk

- Příspěvky: 77
- Reputace: 0
- Web
další Limita
Ahoj,
mám problém s dvěma limitami první se mi podařilo spočítat ale nevim jeslti dobře. výsledek mi vyšel
výsledek mi vyšel  tak jestli je výsledek správně
tak jestli je výsledek správně
pak mam druhou tam to má ze zadání vyjít 
a zadání je: 
Offline
#2 12. 10. 2008 13:56
Re: další Limita
Na ten prvni priklad jsem zkusil jit pres L'Hospitalovo pravidlo:

Jeste by to mohl nekdo preletnout, jestli tam neni nejaka chybka...
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#3 12. 10. 2008 14:54 — Editoval Pavel (12. 10. 2008 15:04)
Re: další Limita
↑ Lishaak:
ve druhé limitě má být místo znaménka  znaménko
znaménko 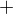 .
.
Obě limity lze řešit bez použití l'Hospitalova pravidla.
Pokud jde o druhou limitu, použil bych vzorec
který pozměním použitím substituce ![kopírovat do textarea $A=\sqrt[3]{a}$](/mathtex/86/86e8ca1a44845cd70a22b89a7482dc73.gif) a
a ![kopírovat do textarea $B=\sqrt[3]{b}$](/mathtex/41/41cf1e727bc18e4069b90ef60c987916.gif) takto:
takto:![kopírovat do textarea $ a-b=(\sqrt[3]{a}-\sqrt[3]{b})(\sqrt[3]{a^2}+\sqrt[3]{ab}+\sqrt[3]{b^2})\qquad\Rightarrow\qquad \sqrt[3]{a}-\sqrt[3]{b}=\frac{a-b}{\sqrt[3]{a^2}+\sqrt[3]{ab}+\sqrt[3]{b^2}} $](/mathtex/9a/9aa9944316ca8aa403cf3b41cdb174cb.gif)
Rozdíl třetích odmocnin ve druhé limitě bych upravil podle tohoto vzorce. Pak stačí upravit čitatele, vytknout nejvyšší mocninu ze jmenovatele a pak už to půjde samo :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 12. 10. 2008 15:14
Re: další Limita
Pavel napsal(a):
ve druhé limitě má být místo znaménka
znaménko
Nesouhlasim. Pokud by tam bylo +, tak se ty vyrazy nebodou rovnat pro x < 0, coz jsou hodnoty o ktere nam jde,
Ale tim rozsirenim je to samozrejme hezci.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#5 12. 10. 2008 15:31
Re: další Limita
↑ Lishaak:
Už to vidím, samozřejmě,
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
