Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Charakteristická funkce (TOTO TÉMA JE VYŘEŠENÉ)
#6 28. 03. 2012 23:55 — Editoval jardofpr (28. 03. 2012 23:58)
Re: Charakteristická funkce
↑ kotry:
ok
vezmeme si množinu 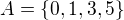
potom jej charakteristická funkcia podľa toho čo som napísal vyššie,
má hodnotu  pre
pre  a inde
a inde 
teda 



ale napríklad  lebo
lebo 
škaredý obrázok
teda charakteristická funkcia podmnožiny reálnych čísel priradí hodnotu 1 každému číslu, ktoré do tej množiny patrí,
hodnotu 0 všetkým ostatným reálnym číslam
chápeš ten princíp?
(na tom strašnom neprehľadnom obrázku je graf charakteristickej funkcie množiny A červenou farbou)
Offline
#7 29. 03. 2012 00:12 — Editoval vanok (29. 03. 2012 00:13)
Re: Charakteristická funkce
Ahoj ↑ jardofpr:,
Len mala otazka, pre ↑ kotry:
Nevideli ste nahodou nejaku takuto vetu:
Ak A a B su disjoktne ( cize bez spolocnych prvkov) mame 
To sa da pouzit aj v tvojom cviceni.... a da ti to vysledok bez namahy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 30. 03. 2012 15:33
Re: Charakteristická funkce
↑ jardofpr:
už asi chápu... takže 
 atd.
atd.
ale když je mám potom sčítat, jako v mém příkladu tak by to byl průnik těch množin? 
takže výsledek toho mého příkladu by byl 0?
Offline
#9 31. 03. 2012 09:42 — Editoval jardofpr (01. 04. 2012 14:48)
Re: Charakteristická funkce
kotry napsal(a):
↑ jardofpr:
takže
atd.
presne tak, ale aj napríklad 
na začiatok je možno dobré si rozpísať ako každá z tých funkcií vyzerá, ak stále tápaš, nakresli si ich


keď sa na to pozrieš bližšie,
malo by byť vidno že funkcia môže mať najviac 2 body nespojitosti,  a
a 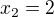 ,
,
lebo na intervaloch  sú všetky tri tieto rôzne charakteristické funkcie konštantné, spojité
sú všetky tri tieto rôzne charakteristické funkcie konštantné, spojité
treba ti teda vyšetriť v podstate len spojitosť v tých dvoch bodoch
tento príklad môžeš aj tak najľahšie urobiť podľa toho čo píše ↑ vanok: o kúsok vyššie, rýchlo zistíš že hľadaná funkcia je konštantná nula definovaná na celej množine reálnych čísel, čo je asi najtriviálnejší príklad funkcie spojitej v každom bode svojho definičného oboru..
pre zoznámenie sa s takýmto typom funkcie môžeš vyšetrovať funkčné hodnoty na každom z tých troch intervalov zvlášť trebárs...
dôležité zistenie bude že 
Offline
#10 01. 04. 2012 11:31
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Charakteristická funkce (TOTO TÉMA JE VYŘEŠENÉ)


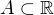 potom
potom 
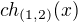 ?
?