Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 04. 2012 11:02
Rekurentně zadaná posloupnost
Zdravím,
potřeboval bych radu, jak nejlépe určit z rekurentně zadané posloupnosti vzorec pro n-tý člen a obráceně. U jednodušších příkladů to zvládám, ale u složitějších už tápu. Není na to nějaký osvědčený recept? Děkuji předem za případné objasnění.
Offline
#3 14. 04. 2012 13:03 — Editoval elypsa (14. 04. 2012 13:09)
Re: Rekurentně zadaná posloupnost
↑ weca:
Ahoj!
Z rekurentního na n-tý člen to je trochu komplikovanější - musí se dokazovat atd.. Zde proto příliš neporadím.
Ale z n-tého členu na rekurentní se to dá zvládnout například pomocí a) podílu  ; b ) rozdílu
; b ) rozdílu 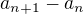
Pozn.: U podílu je třeba dát pozor aby se  nerovnalo nule
nerovnalo nule
Příklad: 
zkusíme například podílem:
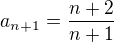

tím jsme teda zjistili že 
takže stačí pouze vynásobit an a máme rekurentní vyjádření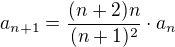
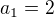
rozdílem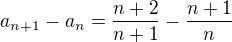
hodíš to na jeden zlomek a upravíš
potom opět jen vyjádříš  :
: 
Baf!
Offline
