Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2012 13:33 — Editoval ivaberánková (15. 04. 2012 13:39)
- ivaberánková

- Příspěvky: 79
- Reputace: 0
přímka a rovina v prostoru
napiste parametrické vyjádření přímky, prochází bodem A a je rovnobezná s přímkou BC
A(9;-3;1) B(-4;-7;6) C(2;-5;3)
tady si taky udelam B-C
Offline
#2 15. 04. 2012 15:01
Re: přímka a rovina v prostoru
Zdravím.
Parametrické vyjádření přímky je 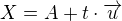 .
.
Bod A leží na přímce,  je směrový vektor přímky.
je směrový vektor přímky.
Pokud má být přímka rovnoběžná s přímkou BC, pak její směrový vektor musí být "rovnoběžný" se směrovým vektorem přímky BC, tedy musí být jejím násobkem.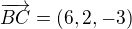
![kopírovat do textarea $A=[9,-3,1]$](/mathtex/4f/4ff2b6b0fddc35e388705f31d1290d8e.gif)
Tedy![kopírovat do textarea $p\equiv X=[9,-3,1]+t\cdot (6,2,-3)$](/mathtex/2e/2eed735998e99541b4690cf5b268148d.gif)
Offline
