Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diagonalizovatelnost matice (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 04. 2012 18:57
Diagonalizovatelnost matice
Ahoj,
řeším úlohu, pro které  je daná matice diagonalizovatelná - tj. pro které parametry
je daná matice diagonalizovatelná - tj. pro které parametry  platí, že pro každé vlastní číslo
platí, že pro každé vlastní číslo  matice platí, že jeho algebraická násobnost (ozn.
matice platí, že jeho algebraická násobnost (ozn. 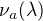 ) je rovna geometrické násobnosti tohoto vlastního čísla ( (ozn.
) je rovna geometrické násobnosti tohoto vlastního čísla ( (ozn. 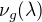 ).
).
Zadání:
Charakteristický polynom je roven 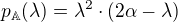 .
.
Rozlišil jsem případy:
1/  a tudíž je
a tudíž je 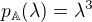 a geometrická násobnost je
a geometrická násobnost je  tj
tj 
Tj. v případě 1/ je diagonalizovatelná
2/ 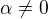 tj budou dvě vlastní čísla :
tj budou dvě vlastní čísla :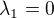 a
a 
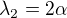 a protože
a protože 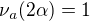 tak i
tak i 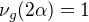 .
.
Tj. i v případě 2/ je diagonalizovatelná
Vychází mi proto, že je diagonalizovatelná  , ve výsledcích však píší, že je diag. jen pro
, ve výsledcích však píší, že je diag. jen pro  ,. Poradíte mi, kde dělám chybu?
,. Poradíte mi, kde dělám chybu?
Děkuji.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#3 30. 04. 2012 15:30
Re: Diagonalizovatelnost matice
↑ Andrejka3: Díky za odpověď, taky si to myslím, zkoušel jsem počítat konkrétně pro různá alfa a fungovalo :).
Offline
#4 30. 04. 2012 15:41
Re: Diagonalizovatelnost matice
↑ Sulfan:
Charakteristická rovnice je správně, diskuze ohledně vlastních čísel taky a dimenze kořenových podprostorů příslušných vlastním číslům (říká se tomu tak, ne?) je taky správně.
Všechno máš hezky zapsané, jen mě ze začátku trochu zmátlo:
dimenze (matice), ale došlo mi, že to je její hodnost a to celé je dimenze 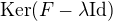 , kde lambda je dané vlastní číslo a F je zkoumaný operátor.
, kde lambda je dané vlastní číslo a F je zkoumaný operátor.
Bohužel, i v dobrých učebnicích jsou chyby. A někdy to může studenty zaseknout :)
Tak ať se daří,
A.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diagonalizovatelnost matice (TOTO TÉMA JE VYŘEŠENÉ)