Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Globální extrémy funkce tří proměnných (bez věty o vázaných extrémech) (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 05. 2012 19:12 — Editoval Mihulik (12. 05. 2012 19:18)
Globální extrémy funkce tří proměnných (bez věty o vázaných extrémech)
Ahoj,
snažím se nalézt globální extrémy funkce  kde
kde ![kopírovat do textarea $x,y,z\in[0,\pi]$](/mathtex/88/884a7bea711fc5ee9ba058be1bf0b5ae.gif) .
.
Pokud možno bych je ale chtěl nalézt bez využití věty o vázaných extrémech.
Můj dosavadní postup:
Definiční obor funkce je kompaktní množina ![kopírovat do textarea $[0,\pi]\times[0,\pi]\times[0,\pi]$](/mathtex/76/76401cdeabddd6f810400dd3ed09c793.gif) a funkce je na této kompaktní množině spojitá, tzn. globální maximum a minimum existuje.
a funkce je na této kompaktní množině spojitá, tzn. globální maximum a minimum existuje.
Glob. extrémy hledáme ve vnitřních bodech množiny, kde vyjdou parc. derivace nulové, nebo neexistují a na hraničních bodech def. oboru. Parc. derivace existují všude a nulové jsou v bodě ![kopírovat do textarea $[\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}]$](/mathtex/89/89a6765d8e923cd98b38fc0936727c0e.gif) (ještě vyjdou nulové v krajních bodech
(ještě vyjdou nulové v krajních bodech ![kopírovat do textarea $[0,0,0]$](/mathtex/24/24e20e791b6df3fc62aa36083ae57992.gif) a
a ![kopírovat do textarea $[\pi,\pi,\pi]$](/mathtex/68/683b34107d571a090dfcc9170e475fb5.gif) , ale to je díky tomu, že technicky pracujeme s touto funkcí jako by byla definována na celém
, ale to je díky tomu, že technicky pracujeme s touto funkcí jako by byla definována na celém  , ale my ji uvažujeme jen na restrikovaném def. oboru, tzn. parc. derivace v těchto krajních bodech na našem def. oboru neexistují, protože zde existují příslušné parc. derivace jen z jedné strany).
, ale my ji uvažujeme jen na restrikovaném def. oboru, tzn. parc. derivace v těchto krajních bodech na našem def. oboru neexistují, protože zde existují příslušné parc. derivace jen z jedné strany).
Snadno ověříme, díky omezenosti funkce sinus, že funkce nabývá v bodě ![kopírovat do textarea $[\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}]$](/mathtex/89/89a6765d8e923cd98b38fc0936727c0e.gif) maxima a že ho nabývá na našem def. oboru právě v tomto bodě. Naše funkce má tedy právě jedno glob. maximum a to v bodě
maxima a že ho nabývá na našem def. oboru právě v tomto bodě. Naše funkce má tedy právě jedno glob. maximum a to v bodě ![kopírovat do textarea $[\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}]$](/mathtex/89/89a6765d8e923cd98b38fc0936727c0e.gif) .
.
Globální minimum (minima) tedy hledáme na krajních bodech. Tady se ale zaseknu. Vyzkouším např. bod ![kopírovat do textarea $[0,0,0]$](/mathtex/24/24e20e791b6df3fc62aa36083ae57992.gif) a zjistím, že funkce tam nabývá nuly. To by intuitivně mohlo být minimum a tak bych potřeboval najít krajní body, kde funkce nabývá nuly, a dokázat, že jinde je ostře větší než 0.
a zjistím, že funkce tam nabývá nuly. To by intuitivně mohlo být minimum a tak bych potřeboval najít krajní body, kde funkce nabývá nuly, a dokázat, že jinde je ostře větší než 0.
Budu-li například uvažovat stěnu krychle (def. obor je vlastně krychle v  ), kde
), kde ![kopírovat do textarea $x,y\in [0,\pi]$](/mathtex/fe/febd3069aae9f8439a90a8abf9ba0165.gif) a
a 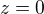 , tak řeším rovnici
, tak řeším rovnici  , ale nevím, jak ji slušně analyticky vyřešit.
, ale nevím, jak ji slušně analyticky vyřešit.
Budu vděčný za případné rady či nasměrování.
Děkuji.
Offline
- (téma jako vyřešené označil(a) Mihulik)
#2 12. 05. 2012 20:04
Re: Globální extrémy funkce tří proměnných (bez věty o vázaných extrémech)
Ono to asi fakt nezáporný bude, ale takovej běžnej způsob je, že si vezmeš jednotlivý krajní množiny, např. tu stěnu z=0, a klasicky vyšetřuješ fci dvou proměnných 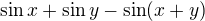 .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Globální extrémy funkce tří proměnných (bez věty o vázaných extrémech) (TOTO TÉMA JE VYŘEŠENÉ)
