Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sestrojitelnost pravidelného sedmiúhelníku
#1 06. 06. 2012 19:05
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Sestrojitelnost pravidelného sedmiúhelníku
Ahoj,
řeším seminárku do algebry. Zadání zní:
Lze sestrojit pomocí pravítka a kružítka pravidelný sedmiúhelník? Dokažte!
Dobrala jsem se kubické rovnice 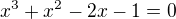
Přes vlastnost, že se polynom třetího stupně dá vyjádřit jako součin lineárního dvojčlenu a polynomu druhého stupně, jsem dostala soustavu rovnic
ac=1
ad+bc=1
ae+bd=-2
be=-1
Postupně jsem vyjádřila a, d, e, dosadila a dostala rovnici
A teď jsem v koncích. Jak mu mám z tohohle vysvětlit, že to nejde sestrojit ...
Offline
#2 06. 06. 2012 19:14
Re: Sestrojitelnost pravidelného sedmiúhelníku
http://cs.wikipedia.org/wiki/Sedmi%C3%BAheln%C3%ADk
tu je pripomenute ze heptagone sa neda presne konstruhovat.
Pozri aj tu
http://cs.wikipedia.org/wiki/Eukleidovs … ln.C3.ADky
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 06. 06. 2012 19:32
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Sestrojitelnost pravidelného sedmiúhelníku
↑ vanok:
To že to nejde sestrojit vím. Ale jak mu to mám z té rovnice dokázat? To je můj problém. Jemu nestačí taková konstatování :-(
Offline
#4 06. 06. 2012 21:14 — Editoval vanok (07. 06. 2012 13:50)
Re: Sestrojitelnost pravidelného sedmiúhelníku
na to je uzitocne aj toto
http://en.wikipedia.org/wiki/Constructible_number
tak si to pozri.
Ten seminar je na akej urovni???
Pochopitelne, ze nemozes pouzit tu Gauss-ovu thm, lebo by sa tza pytali jej dokaz, a ten nie je az tak jednoduchy.
Moje spomienky na tu tvoju rovnicu 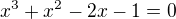 ( ktora sa dostane po upravach z
( ktora sa dostane po upravach z  (polozis x=z+1/z)
(polozis x=z+1/z)
su ze treba dokazat ze tato rovnica ma len irationalne korene:
To sa robi ze polozis x=p/q (p; q nesudelitelne) a dostanes z toho spor.
Dosledok je ze x nie je konstruktiblilny ( preto ani z) ( ale zda sa mi ze na to treba thm od Wantzel-a).
Staci?
Edit:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sestrojitelnost pravidelného sedmiúhelníku
