Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 09. 2012 22:46
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Průměrná četnost lichých čísel v dané množině
Ahoj,
při řešení problému zde mě napadla tato úloha: Jaká je (pro pevné m přirozené) průměrná relativní četnost lichých čísel (označme tento počet jako  ) mezi čísly
) mezi čísly ![kopírovat do textarea $a_i(m) := [ \frac{m}{2^i} ]$](/mathtex/96/960bd8b9024228836dcacc920f0f2be9.gif) pro i celé nezáporné takové, že
pro i celé nezáporné takové, že 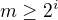 . Např. pro m=5 máme pro i=0,1,2
. Např. pro m=5 máme pro i=0,1,2  =5,2,1, tj. uvedená četnost je
=5,2,1, tj. uvedená četnost je  . Obecně lze úlohu zformulovat tak, že položíme
. Obecně lze úlohu zformulovat tak, že položíme 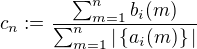 , což je průměrná četnost mezi čísly 1 až n a pak lze hledat hodnotu
, což je průměrná četnost mezi čísly 1 až n a pak lze hledat hodnotu 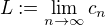 . Úkolem je tedy zjistit hodnotu L.
. Úkolem je tedy zjistit hodnotu L.
Alternativně lze zkoumat hodnotu 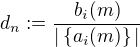 a následně
a následně  a hledat hodnotu K.
a hledat hodnotu K.
Volněji lze úlohu zformulovat tak, že hledáme pravděpodobnost pro náhodné přirozené číslo m a náhodné i, pro které platí 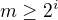 , že
, že ![kopírovat do textarea $[ \frac{m}{2^i} ]$](/mathtex/de/de893664f2205e28d9448184221c015f.gif) je liché.
je liché.
(Úlohu lze zobecnit a místo 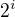 uvažovat libovolnou jinou rostoucí funkci a rovněž místo lichých čísel zkoumat obecně nějakou hodnotu zbytku modulo P pro nějaké přirozené P.)
uvažovat libovolnou jinou rostoucí funkci a rovněž místo lichých čísel zkoumat obecně nějakou hodnotu zbytku modulo P pro nějaké přirozené P.)
"Máte úhel beta." "No to nemám."
Offline
#2 02. 09. 2012 01:50 — Editoval anes (02. 09. 2012 01:52)
Re: Průměrná četnost lichých čísel v dané množině
Ahoj, v tuhle dobu už se nechci moc rozepisovat a nejsem si úplně jistý, jak moc rozumím Tvé otázce, takže tenhle příspěvek ber spíš jako pokus o nasměrování (svedení z cesty? :) ) než o vyřešení.
Já si myslím, že odpověď na většinu tvých otázek je jedna polovina. Vybereme úplně náhodně  (řekněme aspoň
(řekněme aspoň 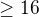 ). K němu bude existovat nějaké
). K němu bude existovat nějaké  , že
, že  .
.
Nevím, jestli to je zajímavé, ale pro sebe si kreslím číselnou osu se třemi body -- 0, 2^i, 2^{i+1}. Bod  byl volený náhodně, takže ho nikam nezanáším, ale představuji si ho rovnoměrně rozmatlaný v tom patřičném intervalu.
byl volený náhodně, takže ho nikam nezanáším, ale představuji si ho rovnoměrně rozmatlaný v tom patřičném intervalu.
Je jasné, že 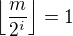 je liché. Pro dělení nižšími mocninami dvojky už to ale bude s paritou 50 na 50 podle toho, jaké máme konkrétní
je liché. Pro dělení nižšími mocninami dvojky už to ale bude s paritou 50 na 50 podle toho, jaké máme konkrétní  .
.
Číslo 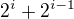 rozdelí interval
rozdelí interval 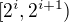 na dvě půlky a parita čísla
na dvě půlky a parita čísla 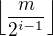 bude záležet na tom, ve které z nich
bude záležet na tom, ve které z nich  leží.
leží.
Když na osu přikreslíme násobky  , interválky si zase rozpůlíme, a opět půlka odpovídá lichým chodnotám
, interválky si zase rozpůlíme, a opět půlka odpovídá lichým chodnotám 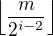 a půlka sudým...
a půlka sudým...
Z toho bych soudil, že (pokud si nějak špatně nevykládám zápis) posloupnost  půjde v limitě dost rychle k jedné polovině. Jak by ty hodnoty
půjde v limitě dost rychle k jedné polovině. Jak by ty hodnoty 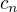 kolísaly mezi těmi mocninami dvojky chce ještě dopromyslet, nevidím teď, jestli by vůbec limita
kolísaly mezi těmi mocninami dvojky chce ještě dopromyslet, nevidím teď, jestli by vůbec limita 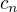 existovala.
existovala.
... a pořád mám pocit, že to nějak moc komplikuji...
Offline
#3 02. 09. 2012 20:10
- check_drummer

- Příspěvky: 5177
- Reputace: 106
Re: Průměrná četnost lichých čísel v dané množině
↑ anes:
Ahoj, mě právě teď napadlo uvažovat všechna m jako by byla psána ve dvojkové soustavě. Pak zkoumaným číslům odpovídá to, že "odřízneme" z čísla m posledních i číslic. Z toho už by skoro mohlo být zřejmé, že sudých bude stejně jako lichcých, protože mezi číslicemi čísel 1 až n se v jejich binárním zápisu bude objevovat 0 stejně často jako 1 (neuvažujeme-li ovšem první číslici, která je vždy 1).
Snad by se tato úvaha dala dotáhnout precizně do konce. Sice není tak pozdě, ale také už dnes nemám myšlenky na rozvádění dalších úvah. :-)
"Máte úhel beta." "No to nemám."
Offline
