Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » neanalytická funkcia s netriviálnym taylorovým radom (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 09. 2012 12:50
neanalytická funkcia s netriviálnym taylorovým radom
ahojte v príkladoch na neanalytické ľubovoľne veľa krát derivovateľné funkcie sa uvádzajú také, ktoré majú nulový taylorov rad existuje taká funkcia čo má netriviálny(nenulový alebo ešte lepšie nekonštantný) taylorov rad pri tom sa mu nerovná na žiadnom okolí stredu radu a ten rad na nejakom okolí(s kladným polomerom) konverguje?
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 26. 09. 2012 12:52 — Editoval Pavel Brožek (26. 09. 2012 12:53)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: neanalytická funkcia s netriviálnym taylorovým radom
↑ jarrro:
Pokud mám tu funkci, která má nulový Taylorův rozvoj, a přičtu k ní polynom, tak dostanu funkci, kterou hledáš. Nebo jsem tě špatně pochopil?
Offline
#3 26. 09. 2012 13:25 — Editoval jarrro (26. 09. 2012 13:35)
Re: neanalytická funkcia s netriviálnym taylorovým radom
↑ Pavel Brožek:aha asi máš pravdu taká funkcia bude mať vú a vyššie derivácie nulovú a taylorov rad bude pripočítaný polynóm díky.
vú a vyššie derivácie nulovú a taylorov rad bude pripočítaný polynóm díky.
a taká funkcia čo by spĺňala  ?
?
asi by mohlo fungovať k funkcii s nulovým radom pripočítať analytickú je to tak? taylorov rad takej funkcie by bol v súčte tá analytická funkcia potom.
je to tak?
teraz ma zase napadlo či každá ľubovoľne veľakrát diferencovateľná funkcia sa dá napísať ako súčet funkcie s nulovým Taylorovým radom a analytickej funkcie aspoň na nejakom hoci aj malom, ale kladnom okolí stredu.
MATH IS THE BEST!!!
Offline
#4 26. 09. 2012 14:12 — Editoval Pavel Brožek (26. 09. 2012 14:44)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: neanalytická funkcia s netriviálnym taylorovým radom
↑ jarrro:
Přesně tak.
Ze zápisu
je vidět, že každou hladkou funkci můžu napsat jako součet funkce, která má nulové všechny derivace až do řádu n, a funkce, která je analytická. V případě rozkladu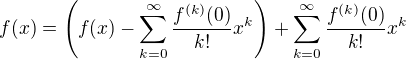
je problém, že by řada nemusela pro nenulová x konvergovat. Nic víc mě teď nenapadá.
Edit: Třeba pro funkci 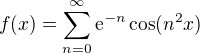 to fungovat nebude, protože její Taylorova řada nekonverguje nikde kromě x=0.
to fungovat nebude, protože její Taylorova řada nekonverguje nikde kromě x=0.
Offline
#5 26. 09. 2012 18:29
Re: neanalytická funkcia s netriviálnym taylorovým radom
Ahoj,
Co si myslis o tejto funkcii pre
pre  a
a  ?
?
(uvazuj Taylorov rozvoj v 0)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 26. 09. 2012 19:11
Re: neanalytická funkcia s netriviálnym taylorovým radom
↑ jarrro:
Ano, a tak jej Taylorov rad nie je dana funkcia!
Cize aj tuto funkciu mozes ako ti radi kolega ↑ Pavel Brožek: (ktoreho pozdravujem).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 26. 09. 2012 19:22
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: neanalytická funkcia s netriviálnym taylorovým radom
↑ vanok:
Zdravím,
ale o tom se tu myslím nebavíme, nehledáme funkci, která se jen liší od svého Taylorova rozvoje. Předpokládám, že tuto funkci jarrro zná, sám ji nejspíš měl na mysli ve svém prvním příspěvku když psal o neanalytických funkcích s nulovým Taylorovým rozvojem.
Otázka, kterou tu teď řešíme, je podle mě následující:
Je možné funkci, která je v bodě x nekonečněkrát diferencovatelná, zapsat jako součet dvou funkcí, z nichž jedna bude mít v bodě x nulovou Taylorovu řadu a druhá bude na nějakém okolí bodu x analytická?
Offline
#9 26. 09. 2012 19:32
Re: neanalytická funkcia s netriviálnym taylorovým radom
↑ Pavel Brožek:áno momentálne je taká otázka.otázku existencie funkcie s nenulovým Taylorom, ale rôznym od danej funkcie sme už myslím rozriešili↑ tu:, ↑ tu: a ↑ tu:
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » neanalytická funkcia s netriviálnym taylorovým radom (TOTO TÉMA JE VYŘEŠENÉ)