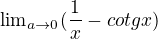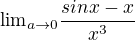Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limity s L´Hospitalem (TOTO TÉMA JE VYŘEŠENÉ)
#2 23. 11. 2008 18:45
Re: Limity s L´Hospitalem
první limita: limita má tvar (fx - gx)=(nekonečno - nekonečno), nemůžeme použít L´hospitala, musíme výraz upravit na tvar lim[(1/gx - 1/fx)/(1/(fx*gx))], tím získáme tvar [(1/cotgx - x)/(x/cotgx)]=0/0 a na tu už můžeme použít L´hospitala
druhá limita: L´hospital= derivace čitatele a jmenovatele -> lim[(cosx-1)/3x^2], tím jsme si moc nepomohli, takže opakujeme ještě jednou L´hospitala -> lim[(-sinx)/6x], pět to není řešitelné, ještě jednou použijeme L´hospitala -> lim[(-cosx)/6]. výsledek limity je -1/6.
Offline
#3 23. 11. 2008 18:53 — Editoval kaja.marik (23. 11. 2008 18:55)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Limity s L´Hospitalem
prvni limita: jednodussi je napsat cotangens jako zlomek cos(x)/sin(x) nebo 1/tan(x) a secist to jako dva zlomky - nebudeme potom derivovat podil (derivace podilu je jeste hnusnejsi podil).
Ktera z tech mych dvou navrhovanych moznosti vede na jednodussi pocitani se asi bez toho aby to clovek zkusil poznat neda.
http://user.mendelu.cz/marik/lhospital-k.pdf - priklad 40 a priklady 10 a 27 (nejak to tam probublalo dvakrat)
Pred druhym pouzitim lhospitalova pravidla v priklade 27 je lepsi vytahnout kosinus ze jmenovatele pred limitu jako jednicku - nebudeme muset derivovat soucin.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limity s L´Hospitalem (TOTO TÉMA JE VYŘEŠENÉ)